FindMatrixGameStrategies[mgame]
finds an optimal strategy profile (Nash equilibrium) for the MatrixGame mgame.
FindMatrixGameStrategies[mgame,spec]
finds strategy profiles following the specification spec.


FindMatrixGameStrategies
FindMatrixGameStrategies[mgame]
finds an optimal strategy profile (Nash equilibrium) for the MatrixGame mgame.
FindMatrixGameStrategies[mgame,spec]
finds strategy profiles following the specification spec.
Details and Options

- FindMatrixGameStrategies is also known as solving a game or finding optimal game strategies such as Nash equilibria.
- Optimal game strategies are typically used as a way to play a game or compute what the expected payoffs are from playing a game.
- FindMatrixGameStrategies returns a list of game strategies.
- A strategy profile
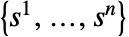 is a Nash equilibrium if all players simultaneously maximize their payoff. Or, equivalently, no player can improve their expected payoff by changing their strategy.
is a Nash equilibrium if all players simultaneously maximize their payoff. Or, equivalently, no player can improve their expected payoff by changing their strategy. - A strategy profile is given by
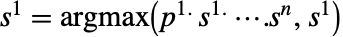 , …,
, …,  , where each maximization takes the strategy
, where each maximization takes the strategy 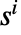 to be a probability vector.
to be a probability vector. - Every matrix game has a Nash equilibrium in the form of a mixed strategy and typically has many.
- Possible specifications spec include:
-
"Mixed" a probability mixture of actions "Pure" a single action - FindMatrixGameStrategies has the following option:
-
Method "SolveValues" what method to use - Possible Method settings include:
-
"FindInstance" use FindInstance on polynomial equations {"FindInstance",n} find 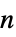 polynomial solutions
polynomial solutions"NSolveValues" use NSolveValues on polynomial equations "SolveValues" use SolveValues on polynomial equations
Examples
open all close allBasic Examples (5)
Find the Nash equilibrium in the Prisoner's Dilemma:
This strategy corresponds to both players always choosing "Defect":
Find the Nash equilibria in the Chicken game:
To obtain only the mixed strategies, use the "Mixed" specification:
Find the Nash equilibria in the Volunteer's Dilemma game:
To obtain only the pure strategies, use the "Pure" specification:
Some games have an infinite number of solutions. Consider the following matrix game:
Find a few Nash equilibria for the game:
Scope (5)
Basic Uses (3)
Find the Nash equilibrium in a Diner's Dilemma game:
Find a Nash equilibrium in the Battle of the Bismarck game:
Determine to which actions this corresponds:
Since an infinite number of solutions is possible, consider finding only 3 Nash equilibria:
Find the Nash equilibrium in the Rock Paper Scissors game:
This corresponds to both players randomly choosing among rock, paper and scissors:
Options (1)
Method (1)
You can use the default SolveValues method:
Use the NSolveValues method:
Use the FindInstance method:
Applications (8)
Social Games (2)
The Volunteer's Dilemma describes a situation where each player can either volunteer or defect. If at least one player volunteers, all other players marginally benefit from defecting. If no player volunteers, all players have a very low payoff. Generate a Volunteer's Dilemma game with 4 players:
The Volunteer's Dilemma has a Nash equilibrium in many cases where it is most probable exactly one player volunteers. Find the optimal game strategies in this game:
The Discoordination game is a hybrid form of coordination and anti-coordination games, where one player's incentive is to coordinate while the other player tries to avoid this. Generate a Discoordination game with a volunteer and a detractor:
Economics Games (3)
Three hungry men go to a restaurant and decide to split the bill evenly. There are three meal options, Cheap, Average and Expensive. Represent this situation as a MatrixGame:
The Cournot Oligopoly game describes a situation where a group of firms produces the same good. Each firm must consider the production cost and the quantity the other firms are producing. Only the firms with the lowest price sell goods. Generate a Cournot Oligopoly game:
Find the optimal game strategies in this game:
This is intuitive when considering that for all players, the payoffs are largest for the second action:
A price war refers to a game where multiple firms have an interest in offering the lowest price, but the payoff of any firm is directly correlated to the price chosen. Consider a price war among 3 firms where each firm has the choice between a low price and a high price:
Despite the common interest of having the price as high as possible, competition creates a Nash equilibrium at the low price:
Military Games (1)
The Colonel Blotto game describes a situation where officers (players) are tasked to simultaneously distribute limited resources over several objects (battlefields). The player devoting the most resources to a battlefield wins that battlefield, and the gain (or payoff) is equal to the total number of battlefields won. Generate a Colonel Blotto game:
Find the optimal strategies in this game:
This is intuitive, considering the second player has more resources, though spreading the resources increases the probable number of battlefields where the player can win:
Recreational Games (1)
Symmetry in Games (1)
Neat Examples (2)
Related Guides
History
Text
Wolfram Research (2025), FindMatrixGameStrategies, Wolfram Language function, https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html.
CMS
Wolfram Language. 2025. "FindMatrixGameStrategies." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html.
APA
Wolfram Language. (2025). FindMatrixGameStrategies. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html
BibTeX
@misc{reference.wolfram_2025_findmatrixgamestrategies, author="Wolfram Research", title="{FindMatrixGameStrategies}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_findmatrixgamestrategies, organization={Wolfram Research}, title={FindMatrixGameStrategies}, year={2025}, url={https://reference.wolfram.com/language/ref/FindMatrixGameStrategies.html}, note=[Accessed: 06-March-2026]}