HammingWindow

HammingWindow[x]

x のハミング窓関数を表す．

詳細

  • HammingWindowは，一般に，電気通信アプリケーションにおけるパルス整形や有限インパルス応答(FIR)フィルタの設計，スペクトル分析で使われる窓関数である．
  • 窓関数は，データが短いセグメントで処理されるアプリケーションに使われ，データ値を漸減して各セグメントの終りで0に近付ける平滑化効果がある．
  • HammingWindow[x]は (21)/(46) cos(2 pi x)+(25)/(46) -1/2<=x<=1/2; 0 TemplateBox[{x}, Abs]>1/2; に等しい．
  • HammingWindowは自動的にリストに縫い込まれる．

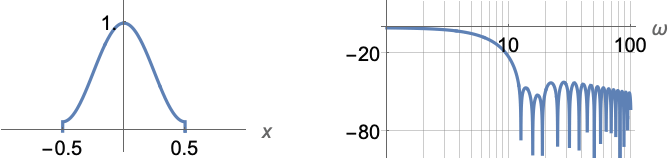
例題

すべて開くすべて閉じる

例  (3)

1Dハミング窓の形：

2Dハミング窓の形：

ハミング窓を表す連続関数を抽出する：

スコープ  (4)

数値的に評価する：

平行移動され広げられたハミング窓：

円形の台を持つ2Dハミング窓：

長さ15の離散ハミング窓：

15×10の2D離散ハミング窓：

アプリケーション  (3)

長さ21の移動平均フィルタを作る：

ハミング窓を使ってフィルタを漸減させる：

フィルタのパワースペクトルの対数振幅プロット：

窓指定を使ってサンプルPowerSpectralDensityを計算する：

スペクトルを計算する：

窓関数を使わずに計算されたスペクトル密度と比較する：

プロットは，窓がスペクトル密度を平坦化したことを示している：

この過程の理論的なスペクトル密度と比較する：

時系列推定に窓指定を使う：

スペクトル推定器に窓を指定する：

特性と関係  (4)

ハミング窓の下の面積：

正規化することで単位面積の窓を作る：

ハミング窓のフーリエ変換：

ハミング窓のパワースペクトル：

長さ11の離散ハミング窓の離散時間フーリエ変換：

ω=0における振幅：

振幅スペクトル：

ハミング窓と矩形窓のパワースペクトル：

Wolfram Research (2012), HammingWindow, Wolfram言語関数， https://reference.wolfram.com/language/ref/HammingWindow.html.

テキスト

Wolfram Research (2012), HammingWindow, Wolfram言語関数， https://reference.wolfram.com/language/ref/HammingWindow.html.

CMS

Wolfram Language. 2012. "HammingWindow." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HammingWindow.html.

APA

Wolfram Language. (2012). HammingWindow. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HammingWindow.html

BibTeX

@misc{reference.wolfram_2024_hammingwindow, author="Wolfram Research", title="{HammingWindow}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/HammingWindow.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hammingwindow, organization={Wolfram Research}, title={HammingWindow}, year={2012}, url={https://reference.wolfram.com/language/ref/HammingWindow.html}, note=[Accessed: 17-November-2024 ]}