ImplicitD
ImplicitD[eqn,y,x]
変数 y が方程式 eqn で定義された陰関数を表していると仮定して,偏導関数 ![]() を与える.
を与える.
ImplicitD[f,eqn,y,x]
変数 y が方程式 eqn で定義された陰関数を表していると仮定して,偏導関数 ![]() を与える.
を与える.
ImplicitD[f,{eqn1,…,eqnk},{y1,…,yk},x]
変数 y1,…,ykが方程式系 eqn1∧…∧eqnkで定義された陰関数を表していると仮定して,偏導関数 ![]() を与える.
を与える.
ImplicitD[f,eqns,ys,{x,n}]
高階導関数 ![]() を与える.
を与える.
ImplicitD[f,eqns,ys,x1,x2,…]
偏導関数 ![]() を与える.
を与える.
ImplicitD[f,eqns,ys,{x1,n1},{x2,n2},…]
高階偏導関数![]() を与える.
を与える.
ImplicitD[f,eqns,ys,{{x1,x2,…}}]
スカラー f に対してベクトル導関数![]() を与える.
を与える.
ImplicitD[f,eqns,ys,{array}]
配列導関数を与える.
詳細



- ImplicitDは,通常,陰的に定義された関数の導関数を計算するために使われる.
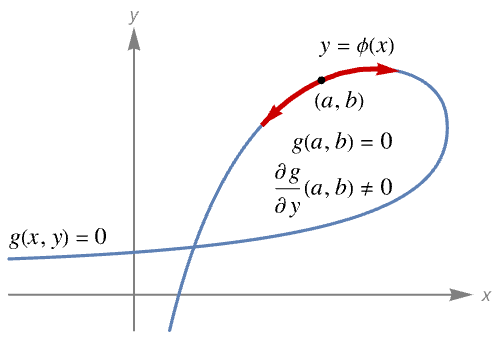
- 変数 x および y が方程式
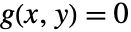 を満足するなら,以下に示した特定の条件下で y は局所的に x の関数として扱うことができ,その関数の導関数は g の偏導関数によって表すことができる.
を満足するなら,以下に示した特定の条件下で y は局所的に x の関数として扱うことができ,その関数の導関数は g の偏導関数によって表すことができる. - 関数
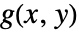 が連続的に微分可能なら,
が連続的に微分可能なら,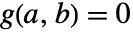 かつ
かつ 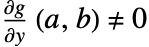 であり,陰関数定理は
であり,陰関数定理は 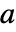 の近傍に
の近傍に 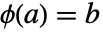 かつ
かつ 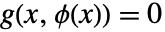 であるような一意の関数
であるような一意の関数 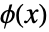 が存在することを保証する.
が存在することを保証する.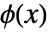 は方程式
は方程式 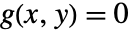 によって定義された陰関数と呼ばれる.したがって,
によって定義された陰関数と呼ばれる.したがって,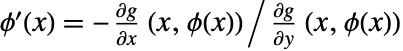 である.
である. - ImplicitD[f,g==0,y,…]は,
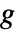 は連続的に微分可能で
は連続的に微分可能で 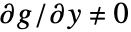 を必要すると仮定する.
を必要すると仮定する. - 同様に,
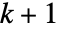 個の変数
個の変数 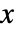 と
と  が
が 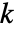 個の方程式の系
個の方程式の系 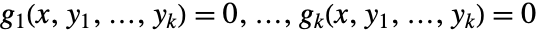 を満足するなら,以下に示した特定の条件下で
を満足するなら,以下に示した特定の条件下で  は局所的に
は局所的に 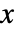 の関数として扱うことができ,それらの関数の導関数は
の関数として扱うことができ,それらの関数の導関数は  の偏導関数によって表すことができる.
の偏導関数によって表すことができる. - 関数
 が連続的に微分可能であるなら,
が連続的に微分可能であるなら, でありヤコビ行列
でありヤコビ行列 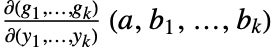 は可逆である.したがって,陰関数定理は
は可逆である.したがって,陰関数定理は 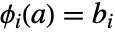 かつ
かつ 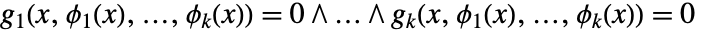 となるような一意の関数
となるような一意の関数 が
が 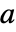 の近傍に存在することを保証する.関数
の近傍に存在することを保証する.関数  は方程式
は方程式  によって定義された陰関数と呼ばれる.したがって,
によって定義された陰関数と呼ばれる.したがって,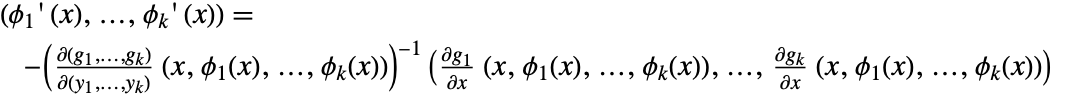 である.
である. - ImplicitD[f,{g1==0,…,gk==0},{y1,…,yk},…]は
 が連続的に微分可能でありヤコビ行列
が連続的に微分可能でありヤコビ行列 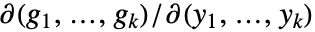 が可逆でなければならないと仮定する..
が可逆でなければならないと仮定する.. - ImplicitD[{f1,f2,…},…]は,リストについては{ImplicitD[f1,…],ImplicitD[f2,…],…}に再帰的に等しい.
- ImplicitD[eqns,ys,…](ここで eqns は方程式または方程式のリストである)はImplicitD[ys,eqns,ys,…]に等しい.
- ImplicitD[f,eqns,ys,{array}]は.事実上,ImplicitDを array の各要素に縫い込む.
- 微分変数あるいは陰関数を表す変数に明示的に依存しない式の偏導関数はすべて0であると解釈される.
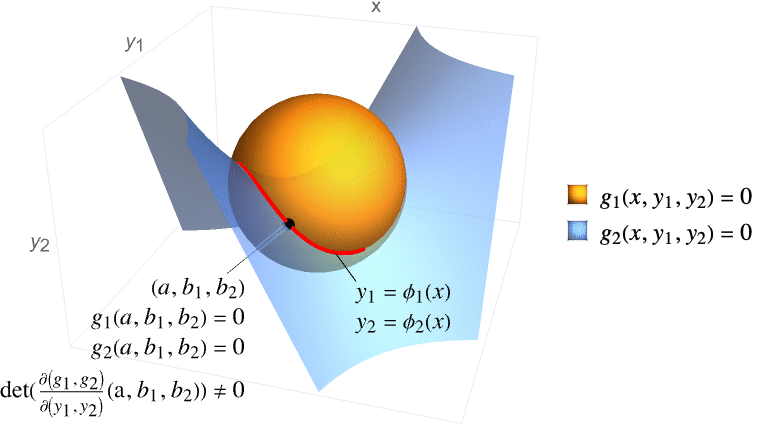
例題
すべて開くすべて閉じる例 (5)
スコープ (9)
アプリケーション (3)
特性と関係 (4)
考えられる問題 (1)
テキスト
Wolfram Research (2022), ImplicitD, Wolfram言語関数, https://reference.wolfram.com/language/ref/ImplicitD.html.
CMS
Wolfram Language. 2022. "ImplicitD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ImplicitD.html.
APA
Wolfram Language. (2022). ImplicitD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImplicitD.html