ImplicitD
ImplicitD[eqn,y,x]
gives the partial derivative 
, assuming that the variable y represents an implicit function defined by the equation eqn.
ImplicitD[f,eqn,y,x]
gives the partial derivative 
, assuming that the variable y represents an implicit function defined by the equation eqn.
ImplicitD[f,{eqn1,…,eqnk},{y1,…,yk},x]
gives the partial derivative 
, assuming that the variables y1,…,yk represent implicit functions defined by the system of equations eqn1∧…∧eqnk.
ImplicitD[f,eqns,ys,{x,n}]
gives the multiple derivative 
.
ImplicitD[f,eqns,ys,x1,x2,…]
gives the partial derivative 
.
ImplicitD[f,eqns,ys,{x1,n1},{x2,n2},…]
gives the multiple partial derivative 
.
ImplicitD[f,eqns,ys,{{x1,x2,…}}]
for a scalar f gives the vector derivative 
.
ImplicitD[f,eqns,ys,{array}]
gives an array derivative.
Details
- ImplicitD is typically used to compute derivatives of implicitly defined functions.
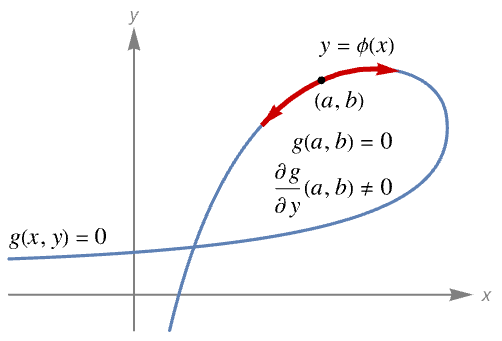
- If variables x and y satisfy an equation
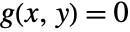, then, under certain conditions spelled out in the following, y can be locally treated as a function of x, and the derivative of this function can be expressed in terms of partial derivatives of g. - If a function
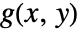is continuously differentiable, 
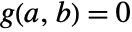and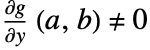 
, then the implicit function theorem guarantees that in a neighborhood of 
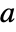there is a unique function 
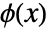such that 
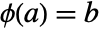and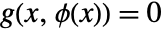 
. 
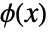is called an implicit function defined by the equation 
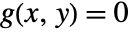. Thus, 
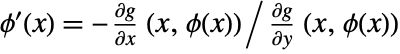. - ImplicitD[f,g==0,y,…] assumes that
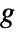is continuously differentiable and requires that 
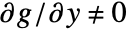. - Similarly, if
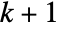variables 
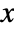and 
satisfy a system of 
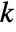equations 
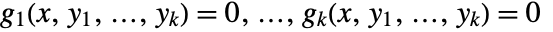then, under certain conditions spelled out in the following, 
can be locally treated as functions of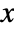 
, and the derivatives of these functions can be expressed in terms of partial derivatives of 
. - If functions
are continuously differentiable, 
and the Jacobian matrix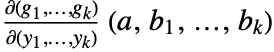 
is invertible, then the implicit function theorem guarantees that in a neighborhood of 
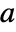, there are unique functions 
such that 
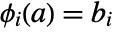and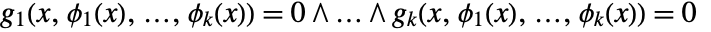 
. Functions 
are called implicit functions defined by the equations 
. Thus,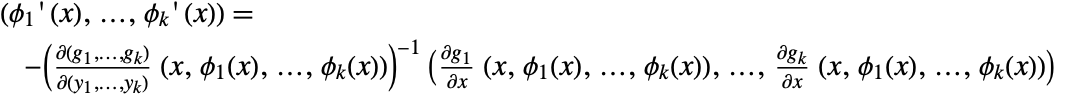 
. - ImplicitD[f,{g1==0,…,gk==0},{y1,…,yk},…] assumes that
are continuously differentiable and requires that the Jacobian matrix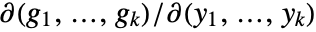 
is invertible. - For lists, ImplicitD[{f1,f2,…},…] is equivalent to {ImplicitD[f1,…],ImplicitD[f2,…],…}, recursively.
- ImplicitD[eqns,ys,…], where eqns is an equation or a list of equations, is equivalent to ImplicitD[ys,eqns,ys,…].
- ImplicitD[f,eqns,ys,{array}] effectively threads ImplicitD over each element of array.
- All expressions that do not explicitly depend on the differentiation variable or on the variables representing implicit functions are taken to have zero partial derivative.
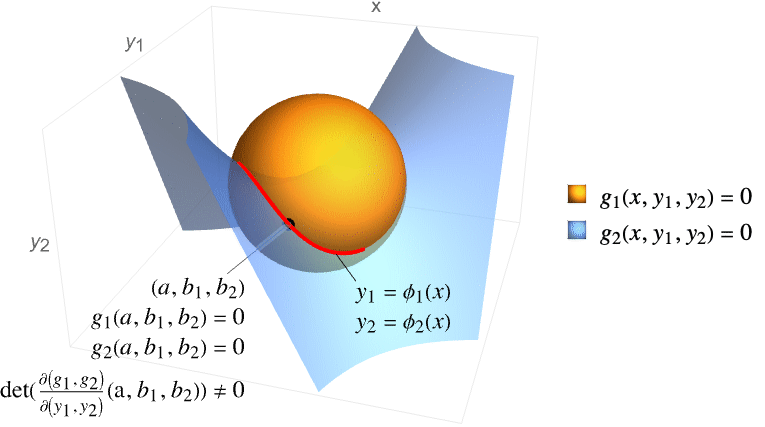
Examples
open allclose allBasic Examples (5)
Scope (9)
Derivative of an implicitly defined function:
Derivative of an expression involving an implicit function defined by a polynomial equation:
Derivative of an expression involving an implicit function defined by a transcendental equation:
Derivative of an expression involving two implicit functions defined by a pair of equations:
Third derivative of an expression involving an implicit function:
The mixed partial derivative 
of an expression involving an implicit function:
The mixed partial derivative 
:
Gradient of an expression involving an implicit function:
Jacobian of an expression involving an implicit function:
Equation defining an implicit function 
needs to have a nonzero derivative with respect to 
:
Equations defining implicit functions 
need to have an invertible Jacobian with respect to 
:
Applications (3)
Compute the slope of the tangent line to a curve:
The slope of the tangent line is equal to the derivative of 
with respect to 
:
Show tangent lines at six points on the curve:
Find tangent planes to a surface:
Compute the gradient of 
with respect to 
and 
:
Show tangent planes at three points on the surface:
Verify an implicit solution to a differential equation:
The derivative of the solution is equal to the right-hand side of the differential equation:
Properties & Relations (4)
Equation 
defines an implicit function in a neighborhood of any point where 
:
The derivative of the implicit function equals 
:
The derivative has singularities at points where 
:
Compute the derivative of an implicit function using D:
Compare with the result obtained using ImplicitD:
Use SolveValues to find an explicit solution of 
:
Compare the derivative of the solution with the result obtained using ImplicitD:
Root[g,k] represents a solution of g[y]:
Compare the derivative of 
with the result obtained using ImplicitD:
Possible Issues (1)
Text
Wolfram Research (2022), ImplicitD, Wolfram Language function, https://reference.wolfram.com/language/ref/ImplicitD.html.
CMS
Wolfram Language. 2022. "ImplicitD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ImplicitD.html.
APA
Wolfram Language. (2022). ImplicitD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImplicitD.html