ImplicitD[eqn,y,x]
给出偏导数 ![]() ,假定变量 y 表示由方程 eqn 定义的隐函数.
,假定变量 y 表示由方程 eqn 定义的隐函数.
ImplicitD[f,eqn,y,x]
给出偏导数 ![]() ,假定变量 y 表示由方程 eqn 定义的隐函数.
,假定变量 y 表示由方程 eqn 定义的隐函数.
ImplicitD[f,{eqn1,…,eqnk},{y1,…,yk},x]
给出偏导数 ![]() ,假定变量 y1,…,yk 表示由方程组 eqn1∧…∧eqnk 定义的隐函数.
,假定变量 y1,…,yk 表示由方程组 eqn1∧…∧eqnk 定义的隐函数.
ImplicitD[f,eqns,ys,{x,n}]
给出多重导数 ![]() .
.
ImplicitD[f,eqns,ys,x1,x2,…]
给出偏导数 ![]() .
.
ImplicitD[f,eqns,ys,{x1,n1},{x2,n2},…]
给出多重偏导数 ![]() .
.
ImplicitD[f,eqns,ys,{{x1,x2,…}}]
对于标量 f 给出向量导数 ![]() .
.
ImplicitD[f,eqns,ys,{array}]
给出一个数组导数.


ImplicitD
ImplicitD[eqn,y,x]
给出偏导数 ![]() ,假定变量 y 表示由方程 eqn 定义的隐函数.
,假定变量 y 表示由方程 eqn 定义的隐函数.
ImplicitD[f,eqn,y,x]
给出偏导数 ![]() ,假定变量 y 表示由方程 eqn 定义的隐函数.
,假定变量 y 表示由方程 eqn 定义的隐函数.
ImplicitD[f,{eqn1,…,eqnk},{y1,…,yk},x]
给出偏导数 ![]() ,假定变量 y1,…,yk 表示由方程组 eqn1∧…∧eqnk 定义的隐函数.
,假定变量 y1,…,yk 表示由方程组 eqn1∧…∧eqnk 定义的隐函数.
ImplicitD[f,eqns,ys,{x,n}]
给出多重导数 ![]() .
.
ImplicitD[f,eqns,ys,x1,x2,…]
给出偏导数 ![]() .
.
ImplicitD[f,eqns,ys,{x1,n1},{x2,n2},…]
给出多重偏导数 ![]() .
.
ImplicitD[f,eqns,ys,{{x1,x2,…}}]
对于标量 f 给出向量导数 ![]() .
.
ImplicitD[f,eqns,ys,{array}]
给出一个数组导数.
更多信息



- ImplicitD 通常用于计算隐式定义函数的导数.
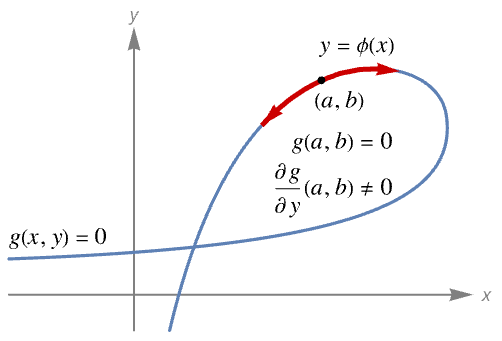
- 如果变量 x 和 y 满足方程
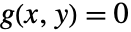 ,则在下面阐述的某些条件下,y 可以被局部视为 x 的函数,并且该函数的导数可以用 g 的偏导数表示.
,则在下面阐述的某些条件下,y 可以被局部视为 x 的函数,并且该函数的导数可以用 g 的偏导数表示. - 如果函数
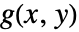 是连续可微的,
是连续可微的,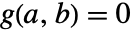 和
和 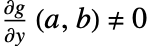 ,则隐函数定理保证在
,则隐函数定理保证在 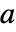 的邻域中存在唯一函数
的邻域中存在唯一函数 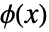 ,使得
,使得 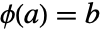 且
且 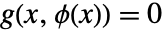 .
. 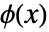 被称为由方程
被称为由方程 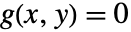 定义的隐函数. 因此,
定义的隐函数. 因此,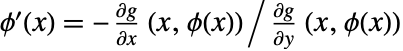 .
. - ImplicitD[f,g==0,y,…] 假定
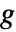 是连续可微的并且要求
是连续可微的并且要求 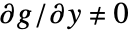 .
. - 类似地,如果
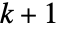 个变量
个变量 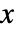 和
和  满足由
满足由 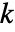 个方程组成的方程组
个方程组成的方程组 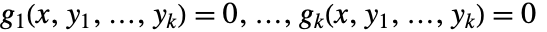 ,则在下述特定条件下,
,则在下述特定条件下, 可以局部视为
可以局部视为 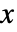 的函数,这些函数的导数可以用
的函数,这些函数的导数可以用  的偏导数表示.
的偏导数表示. - 如果函数
 连续可微,
连续可微, 且雅可比矩阵
且雅可比矩阵 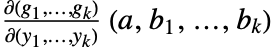 可逆,则隐函数定理保证在
可逆,则隐函数定理保证在 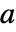 的邻域存在唯一函数
的邻域存在唯一函数  使得
使得 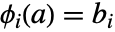 且
且 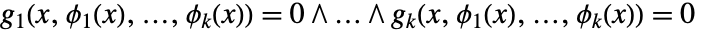 . 函数
. 函数  被称为由方程
被称为由方程  定义的因函数. 因此,
定义的因函数. 因此,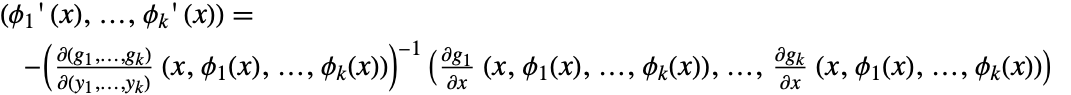 .
. - ImplicitD[f,{g1==0,…,gk==0},{y1,…,yk},…] 假定
 是连续可微的,并且要求雅可比矩阵
是连续可微的,并且要求雅可比矩阵 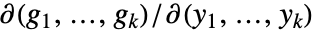 可逆.
可逆. - 对于列表,ImplicitD[{f1,f2,…},…] 递归地等价于 {ImplicitD[f1,…],ImplicitD[f2,…],…}.
- ImplicitD[eqns,ys,…] 等价于 ImplicitD[ys,eqns,ys,…],其中 eqns 是方程或方程的列表.
- ImplicitD[f,eqns,ys,{array}] 有效地将 ImplicitD 遍历 array 的各个元素.
- 所有表达式,只要不显式依赖于微分变量或表示隐函数的变量,都被认为偏导数为零.
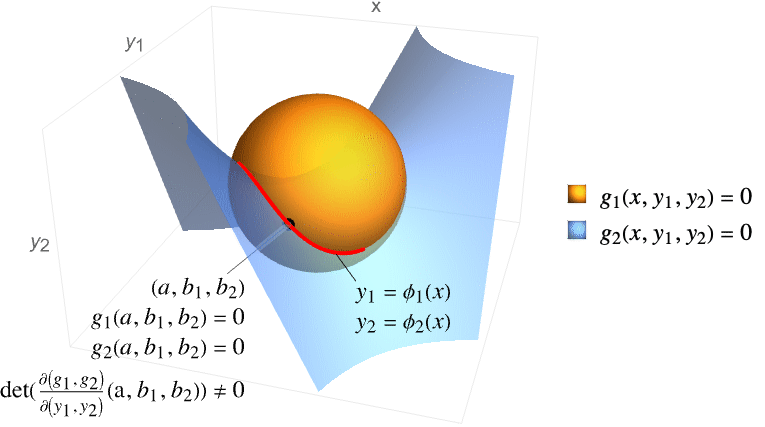
范例
打开所有单元 关闭所有单元范围 (9)
应用 (3)
属性和关系 (4)
可能存在的问题 (1)
相关指南
-
▪
- 微积分
文本
Wolfram Research (2022),ImplicitD,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ImplicitD.html.
CMS
Wolfram 语言. 2022. "ImplicitD." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ImplicitD.html.
APA
Wolfram 语言. (2022). ImplicitD. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ImplicitD.html 年
BibTeX
@misc{reference.wolfram_2025_implicitd, author="Wolfram Research", title="{ImplicitD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ImplicitD.html}", note=[Accessed: 13-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_implicitd, organization={Wolfram Research}, title={ImplicitD}, year={2022}, url={https://reference.wolfram.com/language/ref/ImplicitD.html}, note=[Accessed: 13-February-2026]}