JankoGroupJ2
表示散在 Janko 单群 
.
背景
- JankoGroupJ2[] 表示扬科群
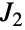，其阶为 ![TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].7](Files/JankoGroupJ2.zh/3.png "TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].7")
. 它是26个有限阶散在单群之一. JankoGroupJ2 的默认表示为具有两个生成器的符号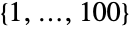 
上的置换群. 
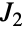也被称作 Hall–Janko 群（表示为 
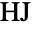）或 Hall–Janko–Wales 群. - 扬科群
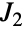是第五小的有限散在单群. 它（连同 JankoGroupJ1 和 JankoGroupJ3）是在1900年代中期由数学家 Zvonimir Janko 发现的，使这些群成为按时间为序第二组被发现的散在群. JankoGroupJ2 是唯一一个作为魔群子商出现的杨科群. 除了置换表示法外，
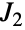可以按生成器和关系的形式定义为
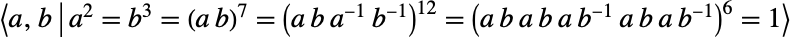. 它包含在康威群 
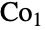中，因此也是唯一一个作为“第二代”散在有限单群的杨科群. 与其它散在单群一样，扬科群在有限单群的巨大（完整）分类中发挥了基础作用. - 通常的群论函数可以应用于 JankoGroupJ2[]，包括 GroupOrder、GroupGenerators 和 GroupElements 等等. 杨科群
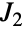的若干预计算属性通过 FiniteGroupData[{"Janko",2},"prop"] 可用. - JankoGroupJ2 与很多其它符号相关. JankoGroupJ2 是统称为“第二代”散在单群的七个群之一（其它六个包括康威群 ConwayGroupCo1、ConwayGroupCo2 和 ConwayGroupCo3，以及 HigmanSimsGroupHS、McLaughlinGroupMcL 和 SuzukiGroupSuz）. 它也是20个所谓“快乐”散在群之一，它们全部作为魔群的子商出现.
范例
Wolfram Research (2010)，JankoGroupJ2，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JankoGroupJ2.html.
文本
Wolfram Research (2010)，JankoGroupJ2，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JankoGroupJ2.html.
CMS
Wolfram 语言. 2010. "JankoGroupJ2." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/JankoGroupJ2.html.
APA
Wolfram 语言. (2010). JankoGroupJ2. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JankoGroupJ2.html 年