JankoGroupJ3
represents the sporadic simple Janko group ![]() .
.
Details
- By default, JankoGroupJ3[] is represented as a permutation group acting on points {1,…,6156}.
Background & Context
- JankoGroupJ3[] represents the Janko group
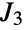 , a group of order
, a group of order ![TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 5}, Superscript].5.17.19 TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 5}, Superscript].5.17.19](Files/JankoGroupJ3.en/3.png) , which is one of the 26 sporadic simple groups of finite order. The default representation of JankoGroupJ3 is as a permutation group on the symbols
, which is one of the 26 sporadic simple groups of finite order. The default representation of JankoGroupJ3 is as a permutation group on the symbols 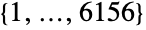 having two generators.
having two generators. - The Janko group
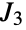 is the eighth smallest of the sporadic finite simple groups. It was discovered (along with JankoGroupJ1 and JankoGroupJ2) by mathematician Zvonimir Janko in the mid 1900s, making these groups tied for second in chronological order of discovery among sporadic groups. JankoGroupJ3 has a modular representation of dimension 18 over the finite field
is the eighth smallest of the sporadic finite simple groups. It was discovered (along with JankoGroupJ1 and JankoGroupJ2) by mathematician Zvonimir Janko in the mid 1900s, making these groups tied for second in chronological order of discovery among sporadic groups. JankoGroupJ3 has a modular representation of dimension 18 over the finite field 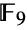 with nine elements. In addition to its permutation representation,
with nine elements. In addition to its permutation representation, 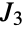 can be defined in terms of generators and relations as
can be defined in terms of generators and relations as 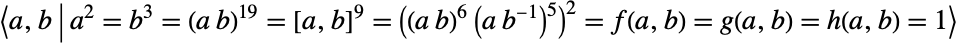 , where
, where 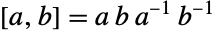 ,
, 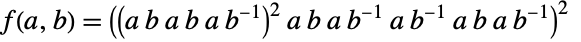 ,
, 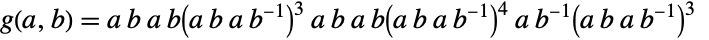 and
and 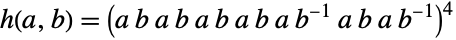 . Along with the other sporadic simple groups, the Janko groups played a foundational role in the monumental (and complete) classification of finite simple groups.
. Along with the other sporadic simple groups, the Janko groups played a foundational role in the monumental (and complete) classification of finite simple groups. - The usual group theoretic functions may be applied to JankoGroupJ3[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Janko group
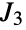 are available via FiniteGroupData[{"Janko",3},"prop"].
are available via FiniteGroupData[{"Janko",3},"prop"]. - JankoGroupJ3 is related to a number of other symbols. Along with JankoGroupJ1, JankoGroupJ4, LyonsGroupLy, ONanGroupON and RudvalisGroupRu (but not JankoGroupJ2), JankoGroupJ3 is one of six sporadic simple groups referred to as "pariahs" as a consequence of their failure to occur as subquotients of the monster group.
Examples
Wolfram Research (2010), JankoGroupJ3, Wolfram Language function, https://reference.wolfram.com/language/ref/JankoGroupJ3.html.
Text
Wolfram Research (2010), JankoGroupJ3, Wolfram Language function, https://reference.wolfram.com/language/ref/JankoGroupJ3.html.
CMS
Wolfram Language. 2010. "JankoGroupJ3." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JankoGroupJ3.html.
APA
Wolfram Language. (2010). JankoGroupJ3. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JankoGroupJ3.html