KroneckerDelta

KroneckerDelta[n1,n2,…]

がすべて等しければ1，そうでなければ0となるクロネッカーのデルタ を与える．

詳細

  • KroneckerDelta[0]は1となり，それ以外の数値 n に対してKroneckerDelta[n]は0となる．
  • KroneckerDeltaは属性Orderlessを持つ．
  • 空のテンプレート 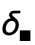は kd で入力することができる．下付き文字内の引数はコンマで区切る．
  • \[InvisibleComma]あるいは,を使ってコンマを不可視にすることができる．
  • KroneckerDeltaは要素単位でリストに縫い込まれる． »

例題

すべて開くすべて閉じる

例  (4)

数値的に評価する：

単位行列を構築する：

総和で使い，要素を抽出する：

整数の部分集合上でプロットする：

スコープ  (26)

数値評価  (6)

数値的に評価する：

複素数入力：

KroneckerDeltaは，入力の精度に関係なく常に厳密な結果を返す：

高精度で効率的に評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のKroneckerDelta関数を計算することもできる：

Aroundを使って平均的な場合の統計区間を計算する：

特定の値  (3)

0における値：

すべての入力が等しいとき，引数が複数の形は1を与える：

記号的に評価する：

可視化  (3)

整数幅のビンを使って1引数のKroneckerDelta関数をプロットする：

KroneckerDeltaを実数上で可視化する．におけるジャンプを除き，ゼロ関数と見分けが付かない：

KroneckerDeltaを三次元でプロットする：

関数の特性  (10)

KroneckerDeltaはすべての実数および複素数の入力について定義される：

KroneckerDelta関数の値域：

複素値についての関数の値域も同じである：

KroneckerDeltaにはリストの入力が使える：

StandardFormとTraditionalFormの両方で従来の表記法が使われている：

KroneckerDeltaは解析関数ではない：

特異点と不連続点の両方を持つ：

KroneckerDeltaは非減少でも非増加でもない：

KroneckerDeltaは単射ではない：

KroneckerDeltaは全射ではない：

KroneckerDeltaは非負である：

KroneckerDeltaは凸でも凹でもない：

微分と積分  (4)

についての一次導関数：

生成点における級数展開：

Integrateを使って不定積分を計算する：

不定積分を確かめる：

その他の積分例：

アプリケーション  (5)

総和で使い，項を抽出する：

2つの上対角を持つ帯行列を生成する：

要素を取り出す：

KroneckerDeltaとLiouvilleLambdaを使ってMoebiusMuを計算する：

球面調和関数を2つの球面調和関数の積の和に分解する：

特性と関係  (2)

KroneckerDeltaを含む方程式を簡約する：

KroneckerDeltaのサポートには測度ゼロが含まれる：

考えられる問題  (2)

KroneckerDeltaは，数値引数のときは，未評価で残されることがある：

$MaxExtraPrecisionの設定値を大きくすることが必要な場合がある：

引数の等価性のテストでは数値精度が考慮される：

おもしろい例題  (1)

符号定数の積をクロネッカーデルタの積の和として表す：

3Dの特殊な場合には，繰り返される指標上での総和が仮定される：

Wolfram Research (1999), KroneckerDelta, Wolfram言語関数， https://reference.wolfram.com/language/ref/KroneckerDelta.html （2017年に更新）.

テキスト

Wolfram Research (1999), KroneckerDelta, Wolfram言語関数， https://reference.wolfram.com/language/ref/KroneckerDelta.html （2017年に更新）.

CMS

Wolfram Language. 1999. "KroneckerDelta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/KroneckerDelta.html.

APA

Wolfram Language. (1999). KroneckerDelta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KroneckerDelta.html

BibTeX

@misc{reference.wolfram_2024_kroneckerdelta, author="Wolfram Research", title="{KroneckerDelta}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/KroneckerDelta.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kroneckerdelta, organization={Wolfram Research}, title={KroneckerDelta}, year={2017}, url={https://reference.wolfram.com/language/ref/KroneckerDelta.html}, note=[Accessed: 21-November-2024 ]}