KroneckerDelta
KroneckerDelta[n1,n2,…]
给出克罗内克 δ 函数 ![]() ,如果所有的
,如果所有的 ![]() 相等,则为1,否则为 0.
相等,则为1,否则为 0.
更多信息
- KroneckerDelta[0] 给出 1;对其它的数值 n,KroneckerDelta[n] 给出 0.
- KroneckerDelta 有属性 Orderless.
- 可以用
 kd
kd 来键入空模板
来键入空模板 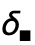 . 应该用逗号把下标中的参数分开.
. 应该用逗号把下标中的参数分开. - 使用字符 \[InvisibleComma] 或
 ,
, 可以使逗号消失.
可以使逗号消失. - KroneckerDelta 自动线性作用于列表. »
范例
打开所有单元关闭所有单元范围 (26)
数值计算 (6)
可视化 (3)
函数属性 (10)
KroneckerDelta 对所有实数和复数输入都有定义:
KroneckerDelta 的值域:
KroneckerDelta 接受列表输入:
在 StandardForm 和 TraditionalForm 中都使用传统的符号:
KroneckerDelta 不是解析函数:
KroneckerDelta 既不是非递增,也不是非递减:
KroneckerDelta 不是单射函数:
KroneckerDelta 不是满射函数:
KroneckerDelta 非负:
KroneckerDelta 既不凸,也不凹:
微分与积分 (4)
应用 (5)
用 KroneckerDelta 和 LiouvilleLambda 计算 MoebiusMu:
属性和关系 (2)
可能存在的问题 (2)
文本
Wolfram Research (1999),KroneckerDelta,Wolfram 语言函数,https://reference.wolfram.com/language/ref/KroneckerDelta.html (更新于 2017 年).
CMS
Wolfram 语言. 1999. "KroneckerDelta." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/KroneckerDelta.html.
APA
Wolfram 语言. (1999). KroneckerDelta. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KroneckerDelta.html 年
