MatrixGamePayoff
MatrixGamePayoff[mgame,{s1,…,sn}]
gives the expected payoff for each player in the matrix game mgame with strategy profile {s1,…,sn}.
MatrixGamePayoff[mgame,{s1,…,sn},"prop"]
gives the payoff property "prop" for each player.
MatrixGamePayoff[mgame,"player1"s1,…,"playern"sn]
gives the expected payoff for each named player in the matrix game mgame with strategy profile {s1,…,sn} using an association.
更多信息

- MatrixGamePayoff is also known as expected payoff or expected utility.
- MatrixGamePayoff is typically used to evaluate expected payoffs for players given strategies for each of the players.
- The strategy profile
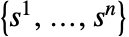 is a list of strategies for the
is a list of strategies for the 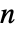 players. Strategy
players. Strategy 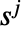 for player
for player 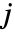 is the vector of probabilities of taking each different action
is the vector of probabilities of taking each different action 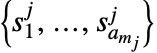 .
. - The expected payoff for player
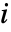 is given by:
is given by:  or
or 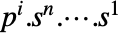 where:
where: -
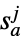
probability for player 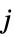 to take action
to take action 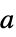
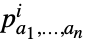
payoff for player 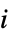 when player
when player 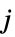 takes action
takes action 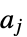
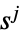
strategy for player 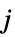
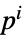
payoff array for player 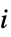
- The payoff properties "prop" include:
-
"Expectation" the average payoff for each player "MarginalDistributions" the distribution of payoffs for each player "MultivariateDistribution" the multivariate distribution of payoffs for all players "Simulation" a randomly generated list of payoffs for a round of the game {"Simulation", n} a list of payoffs for 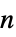 rounds of the game
rounds of the game"Variance" the variance of payoff for each player
范例
打开所有单元关闭所有单元基本范例 (4)
Generate a 2-player matrix game:
Find the expected payoffs for a given strategy:
Generate the 3-coordination game:
Find the expected payoff when the first action is preferred by all players:
Find the expected payoffs for a Prisoner's Dilemma game where both prisoners prefer cooperating:
Generate the 3-coordination game:
Find the expected payoff when the first two players collaborate:
Scope (5)
Generate a 2-player matrix game:
Find the expected payoffs for a given strategy:
Consider a Traveler's Dilemma game for a given strategy:
Find the variances of the payoffs:
Find the marginal distributions:
Find the multivariate distribution:
Generate a Guess Two-Thirds Average game:
Find the expected payoff when the third player is most likely to bet the highest:
Find the expected payoff of the 3-coordination game when the first action is preferred:
Find the expected payoff when the strategies of two groups of two players are correlated:
Find the variances of these correlated strategies:
Find the distributions of these correlated strategies:
Find the multivariate distribution of these correlated strategies:
Simulate 10 rounds repeatedly using these correlated strategies:
Applications (7)
Social Games (2)
The Volunteer's Dilemma describes a situation where each player can either volunteer or defect. If at least one player volunteers, all other players marginally benefit from defecting. If no player volunteers, all players have a very low payoff. Generate a Volunteer's Dilemma game with a volunteer and a detractor:
Find the expected payoffs with a likely volunteer and an unlikely volunteer:
Find the expected payoffs with likely volunteers:
Find the expected payoffs with unlikely volunteers:
The Discoordination game is a hybrid form of coordination and anti-coordination games, where one player's incentive is to coordinate, while the other player tries to avoid this. Generate a Volunteer's Dilemma game with a volunteer and a detractor:
Find the expected payoffs with cooperative players:
Find the expected payoffs with uncooperative players:
Find the expected payoffs with a cooperative player and a uncooperative player:
Economics Games (2)
The Cournot Oligopoly game describes a situation where a group of firms produces the same good. Each firm must consider the production cost and the quantity that the other firms are producing. Only the firms with the lowest price sell goods. Generate a Cournot Oligopoly game:
Find the expected payoffs when the first two players collude:
A price war refers a game where multiple firms have an interest in offering the lowest price, but the payoff of any firm is directly correlated to the price chosen. Consider a price war between 3 firms where each firm has a choice between a low price and a high price:
Clearly, cooperating players have an interest in choosing high prices. Show this by comparing the payoffs of multiple strategies:
Military Games (1)
The Colonel Blotto game describes a situation where officers (players) are tasked to simultaneously distribute limited resources over several objects (battlefields). The player devoting the most resources to a battlefield wins that battlefield, and the gain (or payoff) is equal to the total number of battlefields won. Generate a Colonel Blotto game:
Traffic Games (1)
Amazingly, adding one or more roads to a road network can slow overall traffic, known as Braess's paradox. Given a road network from a to b, taking two different paths either via c or d, the roads ac and db take 20 n minutes where n is the number of drivers on the road, cb and ad take 45 minutes independent of the number of drivers. Represent the road network as a graph:
For two drivers n=2, find all paths from a to b:
Count the number of drivers for each choice of path, which gives four cases:
Find the total time taken for each case:
Maximize the negative commute time:
Create a traffic game based on the payoff matrix:
The two pure strategies correspond to the commuters picking different paths:
These pure strategies also give the shortest commute time of 65 minutes:
Following the traffic game above, you can automate the modeling and solving for a general road network. Here start and end are the start and end vertices, and each road segment capacity is encoded using edge weight:
Add a short high-capacity road segment between d and c:
This situation defines a new traffic game for two drivers:
The new possibility of switching between the two previously existing routes resulted in a Prisoner's Dilemma–like situation, where the only stable solution results in a longer commuting time (82 minutes) compared to the restricted network (65 minutes):
Converging Equilibria (1)
Consider the expected payoff for each player in a two-person game:
Find the expression for each player payoff:
Assume that each player changes their expected payoff following the gradient:
Plot the gradient as a stream plot:
From this plot, you can see that only the pure strategies {{0,1},{1,0}} and {{1,0},{0,1}} are "stable" in the sense that the trajectories converge to them:
Neat Examples (1)
Consider three populations of equal size playing Rock Paper Scissors. Each population either always plays Rock, always Paper or always Scissors. For each game played, if player A loses, then player A adopts the strategy of the adversary. To mimic population growth, after each game, all populations are exponentially increased by 1.02. For a set number of games, the population with the highest percentage is declared the winner:
文本
Wolfram Research (2025),MatrixGamePayoff,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
CMS
Wolfram 语言. 2025. "MatrixGamePayoff." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
APA
Wolfram 语言. (2025). MatrixGamePayoff. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixGamePayoff.html 年