McLaughlinGroupMcL

McLaughlinGroupMcL[]

represents the sporadic simple McLaughlin group .

Details

  • By default, McLaughlinGroupMcL[] is represented as a permutation group acting on points {1,…,275}.

Background & Context

  • McLaughlinGroupMcL[] represents the McLaughlin group 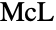, which is a group of order TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 6}, Superscript].TemplateBox[{5, 3}, Superscript].7.11. It is one of the 26 sporadic simple groups of finite order. The default representation of McLaughlinGroupMcL is as a permutation group on the symbols 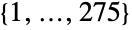having two generators.
  • The McLaughlin group is the tenth smallest of the sporadic finite simple groups. Introduced by mathematician Jack McLaughlin in the late 1960s, McLaughlinGroupMcL is an index-two subgroup of a particular permutation group acting on the so-called McLaughlin graph. In addition to being the only sporadic group to admit irreducible representations of quadratic type, is isomorphic to subgroups of various permutation groups such as ConwayGroupCo2 and ConwayGroupCo3 related to the so-called Leech lattice, and the quotient of by its center is isomorphic to the alternating group AlternatingGroup[8]. Along with the other sporadic simple groups, the McLaughlin group played a foundational role in the monumental (and complete) classification of finite simple groups.
  • The usual group theoretic functions may be applied to McLaughlinGroupMcL[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the McLaughlin group are available via FiniteGroupData["McLaughlin","prop"].
  • McLaughlinGroupMcL is related to a number of other symbols. McLaughlinGroupMcL is one of the seven groups (along with ConwayGroupCo1, ConwayGroupCo2, ConwayGroupCo3, JankoGroupJ2, HigmanSimsGroupHS and SuzukiGroupSuz) cumulatively referred to as the "second generation" of sporadic finite simple groups and is also one of 20 so-called "happy" sporadic groups, which all appear as a subquotient of the monster group.

Examples

Basic Examples  (2)

Order of the group :

Generators of a permutation representation of the group :

Wolfram Research (2010), McLaughlinGroupMcL, Wolfram Language function, https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html.

Text

Wolfram Research (2010), McLaughlinGroupMcL, Wolfram Language function, https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html.

CMS

Wolfram Language. 2010. "McLaughlinGroupMcL." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html.

APA

Wolfram Language. (2010). McLaughlinGroupMcL. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html

BibTeX

@misc{reference.wolfram_2024_mclaughlingroupmcl, author="Wolfram Research", title="{McLaughlinGroupMcL}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mclaughlingroupmcl, organization={Wolfram Research}, title={McLaughlinGroupMcL}, year={2010}, url={https://reference.wolfram.com/language/ref/McLaughlinGroupMcL.html}, note=[Accessed: 17-November-2024 ]}