ONanGroupON
represents the sporadic simple O'Nan group ![]() .
.
Background & Context
- ONanGroupON[] represents the O'Nan group
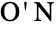 , which is a group of order
, which is a group of order ![TemplateBox[{2, 9}, Superscript].TemplateBox[{3, 4}, Superscript].5.TemplateBox[{7, 3}, Superscript].11.19.31 TemplateBox[{2, 9}, Superscript].TemplateBox[{3, 4}, Superscript].5.TemplateBox[{7, 3}, Superscript].11.19.31](Files/ONanGroupON.en/3.png) . It is one of the 26 sporadic simple groups of finite order and is sometimes known as the O'Nan–Sims group.
. It is one of the 26 sporadic simple groups of finite order and is sometimes known as the O'Nan–Sims group. - The O'Nan group
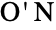 is the thirteenth largest of the sporadic finite simple groups. It was discovered by mathematician Michael O'Nan and constructed explicitly by Charles Sims in the mid-1970s. ONanGroupON was first found while investigating groups having so-called Alperin-type Sylow 2-subgroups. The O'Nan group has a permutation representation on
is the thirteenth largest of the sporadic finite simple groups. It was discovered by mathematician Michael O'Nan and constructed explicitly by Charles Sims in the mid-1970s. ONanGroupON was first found while investigating groups having so-called Alperin-type Sylow 2-subgroups. The O'Nan group has a permutation representation on 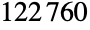 symbols, a triple cover with a pair of 45-dimensional modular representations over field
symbols, a triple cover with a pair of 45-dimensional modular representations over field 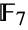 with seven elements, and a number of maximal subgroups, including the Janko group
with seven elements, and a number of maximal subgroups, including the Janko group 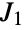 , Mathieu group
, Mathieu group 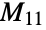 and the alternating group
and the alternating group 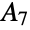 . Along with the other sporadic simple groups,
. Along with the other sporadic simple groups, 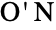 played a foundational role in the monumental (and complete) classification of finite simple groups.
played a foundational role in the monumental (and complete) classification of finite simple groups. - The usual group theoretic functions may be applied to ONanGroupON[], including GroupOrder, GroupGenerators, GroupElements and so on. However, while ONanGroupON[] is a permutation group, due its large order, an explicit permutation representation is impractical for direct implementation. As a result, a number of such group theoretic functions may return unevaluated when applied to it. A number of precomputed properties of the O'Nan group are available via FiniteGroupData["ONan","prop"].
- ONanGroupON is related to a number of other symbols. Along with JankoGroupJ1, JankoGroupJ3, JankoGroupJ4, LyonsGroupLy and RudvalisGroupRu, ONanGroupON is one of six sporadic simple groups referred to as "pariahs" as a consequence of their failure to occur as subquotients of the monster group.
Examples
Wolfram Research (2010), ONanGroupON, Wolfram Language function, https://reference.wolfram.com/language/ref/ONanGroupON.html.
Text
Wolfram Research (2010), ONanGroupON, Wolfram Language function, https://reference.wolfram.com/language/ref/ONanGroupON.html.
CMS
Wolfram Language. 2010. "ONanGroupON." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ONanGroupON.html.
APA
Wolfram Language. (2010). ONanGroupON. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ONanGroupON.html