ObservabilityMatrix

ObservabilityMatrix[ssm]

状態空間モデル ssm の可観測性行列を与える．

詳細

  • 標準的な状態空間モデル
  • 連続時間系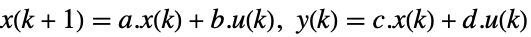
    離散時間系
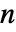  • 可観測性行列はで計算される．ただし， は 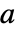の次元である．
  • ディスクリプタ状態空間モデル
  • 連続時間系
    離散時間系
  • KroneckerModelDecompositionに記述されているように，遅い部分系と速い部分系は分離することができる．
  • 遅い部分系
    速い部分系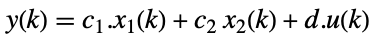
    出力方程式
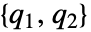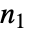  • ObservabilityMatrixは，分離された遅い部分系と速い部分系に基づいて行列のペアを返す．行列 および は以下のように定義される．ただし，は 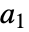の次元であり 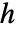は 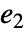のベキ零性指数である．
  • 遅い部分系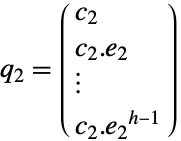
    速い部分系
  • 可観測性行列は，ある λ についてDet[λ e-a]≠0であるディスクリプタ系についてのみ存在する．

例題

すべて開くすべて閉じる

例  (1)

状態空間モデルの可観測性行列：

スコープ  (2)

連続時間系の可観測性行列：

特異系は2つの行列を返す：

特性と関係  (3)

系はその可観測性行列が最大階数であるときかつそのときに限り可観測である：

離散時間系の可観測性行列はサンプリング周期に依存しない：

ディスクリプタ系は，遅い部分系と速い部分系に対して行列を1つずつ返す：

完全な可観測性を持つには，両方の行列が最大階数である必要である：

遅い部分系の可観測性は第1行列で決定される：

Wolfram Research (2010), ObservabilityMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservabilityMatrix.html （2012年に更新）.

テキスト

Wolfram Research (2010), ObservabilityMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservabilityMatrix.html （2012年に更新）.

CMS

Wolfram Language. 2010. "ObservabilityMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/ObservabilityMatrix.html.

APA

Wolfram Language. (2010). ObservabilityMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservabilityMatrix.html

BibTeX

@misc{reference.wolfram_2024_observabilitymatrix, author="Wolfram Research", title="{ObservabilityMatrix}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ObservabilityMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_observabilitymatrix, organization={Wolfram Research}, title={ObservabilityMatrix}, year={2012}, url={https://reference.wolfram.com/language/ref/ObservabilityMatrix.html}, note=[Accessed: 21-November-2024 ]}