ObservabilityMatrix
ObservabilityMatrix[ssm]
gives the observability matrix of the state-space model ssm.
Details
- For a standard state-space model:
-
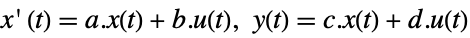
continuous-time system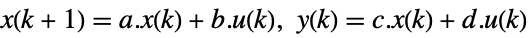 
discrete-time system - The observability matrix is given by
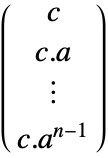, where 
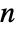is the dimension of 
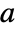. - For a descriptor state-space model:
-
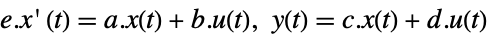
continuous-time system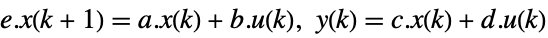 
discrete-time system - The slow and fast subsystems can be decoupled as described in KroneckerModelDecomposition:
-
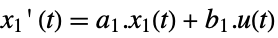
slow subsystem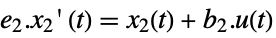 
fast subsystem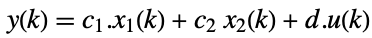 
output equation - ObservabilityMatrix returns a pair of matrices
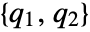, based on the decoupled slow and fast subsystems. The matrices 
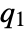and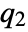 
are defined as follows, where 
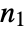is the dimension of 
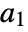, and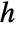 
is the nilpotency index of 
. -
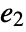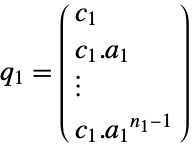
slow subsystem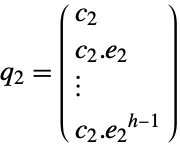 
fast subsystem - The observability matrices only exist for descriptor systems in which Det[λ e-a]≠0 for some λ.
Examples
open all close allScope (2)
Properties & Relations (3)
A system is observable if and only if its observability matrix has full rank:
The observability matrix of a discrete-time system does not depend on the sampling period:
A descriptor system gives one matrix for the slow subsystem and one for the fast subsystem:
Complete observability requires both matrices to be full rank:
Observability of the slow subsystem is determined by the first matrix:
Text
Wolfram Research (2010), ObservabilityMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/ObservabilityMatrix.html (updated 2012).
CMS
Wolfram Language. 2010. "ObservabilityMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/ObservabilityMatrix.html.
APA
Wolfram Language. (2010). ObservabilityMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservabilityMatrix.html