OutputControllabilityMatrix

OutputControllabilityMatrix[ssm]

gives the output controllability matrix of the state-space model ssm.

Details

  • The state-space model ssm can be given as StateSpaceModel[{a,b,c,d}], where a, b, c, and d represent the state, input, output, and transmission matrices in either a continuous-time or a discrete-time system:
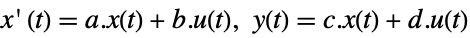
  • continuous-time system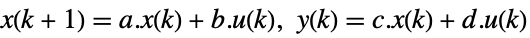
    discrete-time system
  • The output controllability matrix is given by 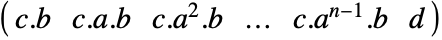, where 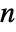is the dimension of the square state matrix .
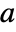  • For a descriptor state-space model, OutputControllabilityMatrix returns a matrix 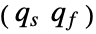where 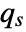is associated with the slow subsystem and 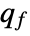is associated with the fast subsystem.
  • For StateSpaceModel[{a,b,c,d,e}] with singular descriptor matrix e, the output controllability matrix is computed by decoupling the slow and fast subsystems:
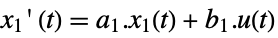
  • slow subsystem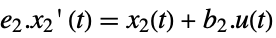
    fast subsystem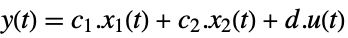
    output equation
  • The output controllability matrix where 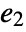has nilpotency index 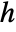is given by .
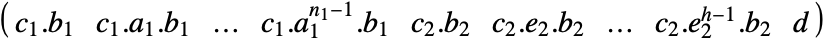  • OutputControllabilityMatrix only takes descriptor systems in which Det[λ e - a]≠0 for some λ.

Examples

open allclose all

Basic Examples  (1)

The output controllability matrix of a state-space model:

Scope  (2)

The output controllability matrix of a continuous-time system:

A descriptor system:

Properties & Relations  (4)

A system is output controllable when the rank of the matrix equals the number of outputs:

This system is not output-controllable but is state-controllable:

This system is output-controllable but not state-controllable:

The output controllability matrix does not depend on the sampling period:

Wolfram Research (2010), OutputControllabilityMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html (updated 2012).

Text

Wolfram Research (2010), OutputControllabilityMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html (updated 2012).

CMS

Wolfram Language. 2010. "OutputControllabilityMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html.

APA

Wolfram Language. (2010). OutputControllabilityMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html

BibTeX

@misc{reference.wolfram_2025_outputcontrollabilitymatrix, author="Wolfram Research", title="{OutputControllabilityMatrix}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_outputcontrollabilitymatrix, organization={Wolfram Research}, title={OutputControllabilityMatrix}, year={2012}, url={https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html}, note=[Accessed: 21-February-2025 ]}