ParametricNDSolveValue

ParametricNDSolveValue[eqns,expr,{x,xmin,xmax},pars]

パラメータが pars，独立変数 x（範囲は xminから xmaxまで）の常微分方程式 eqns の数値解によって決定された関数を使って expr の値を与える．

ParametricNDSolveValue[eqns,expr,{x,xmin,xmax},{y,ymin,ymax},pars]

偏微分方程式 eqns を矩形領域上で解く．

ParametricNDSolveValue[eqns,expr,{x,y}∈Ω,pars]

偏微分方程式 eqns を領域Ω上で解く．

ParametricNDSolveValue[eqns,expr,{t,tmin,tmax},{x,y}∈Ω,pars]

時間依存偏微分方程式 eqns を領域Ω上で解く．

詳細とオプション

  • ParametricNDSolveValueは結果をParametricFunctionオブジェクトによって返す．
  • {pspec1,pspec2,…}のパラメータ pars の指定を使って範囲を指定することができる．
  • pspeciの可能な形式
  • pp は領域RealsまたはComplexesを持つ
    Element[p,Reals]p は領域Realsを持つ
    Element[p,Complexes]p は領域Complexesを持つ
    Element[p,{v1,…}]p は離散範囲{v1,…}を持つ
    {p,pmin,pmax}p の範囲は 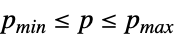である
  • 一般に，expr は微分方程式の解を通してパラメータに間接的に依存しているが，パラメータに明示的に依存していることもある．
  • パラメータについての結果のParametricFunctionオブジェクトの導関数は，可能な場合は数値感度メソッドと記号感度メソッドを組み合せて計算される．
  • ParametricNDSolveValueにはNDSolveと同じオプションと設定が使える．
  • NDSolveとParametricNDSolveValueは，一般に，方程式のタイプによっていくつかの異なる段階に分けて微分方程式を解く．Method->{s1->m1,s2->m2,…}とすると，段階 siがメソッド miで処理される．実際に使われる段階とその順序は，解く問題に基づいてNDSolveによって決定される．
  • 可能な解の段階はNDSolveのものに以下を加えたものである．
  • "ParametricCaching"計算された解をキャッシュする
    "ParametricSensitivity"パラメータについての導関数の計算

    • 全オプションのリスト

例題

すべて開くすべて閉じる

例  (3)

yの値についてのパラメータaのパラメトリック関数を得る：

aの数値で評価するとyについての近似関数解が与えられる：

における値を求める：

パラメータのいくつかの異なる値についての解をプロットする：

における関数fの値を与えるパラメータaの関数を得る：

次は値をパラメータaの関数としてプロットする：

関数をFindRootと一緒に使って根を求める：

微分方程式の解のパラメータについての感度を示す：

aに対する感度はtとともに高くなる：

bについての感度はtとともに高くはならない：

スコープ  (6)

パラメータ依存性  (4)

ParametricNDSolveValueはParametricFunctionオブジェクトを返す：

についての解を得る：

についての解をプロットする：

からまでの の値についての解をプロットする：

初期条件はパラメータとして指定することができる：

で，からまでの の値についての の解をプロットする：

で，からまでの の値についての の解をプロットする：

解 の関数を返す：

：

：

：

：

：

微分方程式の係数と境界条件は，パラメータとして指定できる：

からの範囲の の値に対して で，および で解をプロットする：

パラメータ感度  (2)

パラメータの振幅aを使って古典的な調和振動子を解く：

といくつかの の近傍値についての解をプロットする：

についての の感度は定義によると である．における感度をプロットする：

についての解 の周囲の帯として感度 をプロットする：

複数のパラメータを使った微分方程式の感度解析：

および における という初期条件について感度をプロットする：

および における という初期条件について感度をプロットする：

一般化と拡張  (2)

, をさまざまな値のWorkingPrecisionについて解き，誤差をプロットする：

NDSolveValueが直接解けない，高度に非線形な問題の解を求めることを考える．境界条件，領域，パラメータ に依存する方程式を設定する：

NDSolveValueは解を求めることができない：

初期シード関数を設定する：

パラメータ に基づいてParametricNDSolveValue関数を作成する：

方程式を について解く：

からの解を使うようにシードをリセットする：

リセットしたシードを使って についての解を求める：

解を可視化する：

オプション  (2)

Method  (2)

ParametricCaching  (1)

メモリを保存するために解をキャッシュしないようにする：

キャッシュしないと，必要となる唯一の余分なメモリは処理した方程式のためのものになる：

デフォルトでは直近の計算結果をキャッシュする：

キャッシュすると，必要なメモリ量がはるかに大きくなる：

ParametricSensitivity  (1)

感度は計算しないように指定する：

関数の計算が速くなる：

導関数は計算されていない：

アプリケーション  (14)

パラメータスイープ  (7)

さまざまな高さから落とされて弾むボールのシミュレーションを行う：

微分方程式の解 が となる初期値 を求める：

で解を求める：

結果の解をチェックする：

パラメータsの近くの値と比較する：

境界値問題 , , のいくつかの解を求める．まず，の可能な値をいくつか考える：

パラメータスイープを実行し，の自明ではない解の値を求める：

上記のグラフからの近似初期値を使う：

求まった解をプロットする：

古典的調和振動子 について，のすべての固有値とすべての固有関数 を で求める．可能なパラメータ値を探ることから始める：

の厳密値を求める：

それらをプロットする：

量子的な調和振動子の最初の3つの固有関数，，，lim_(TemplateBox[{x}, Abs]->infty) y(x)=0を求める．まず，についての の解をプロットする：

について をプロットする：

根は近似固有値である．最初の3つを求める：

近似固有関数を近傍の についての解とともにプロットする：

両者は厳密な固有関数であるエルミート関数と倍率が異なるだけである：

, の解が から までの最小弧長になるような の値を求める．0から1までの の値についての解をプロットすることから始める：

に対する解の弧長をプロットする：

での最小の弧長解は にあるように見える：

の近くに現れる極小値を求める：

（局地的）最小弧長に対応する解をいくつかの近傍の解と一緒にプロットする：

時間 における電圧v1でのステップに対するRLC回路の応答のシミュレーションを行う：

成分の値を変えたときのステップ応答を示す：

抵抗rへの依存：

インダクタンスl：

キャパシタンスc：

パラメータ感度  (5)

微分方程式のパラメータに摂動を与え，結果の摂動解をいくつか観察する：

解を感度帯とともにプロットしたものは質的に似ている：

振動数 ω，振幅aで振動している台座上の安定した倒立振子のシミュレーションを行う：

で のとき，振子は倒立位置 近くで安定しているが，感度は上昇する：

Lorenz方程式のパラメータに対する感度を求める：

熱方程式 , のパラメータ依存性：

感度 と を求める：

対応する感度帯をプロットする：

解の曲面の色を変えることでaとcに対する感度を示す：

波動方程式 , におけるパラメータ依存性：

感度とを求める：

対応する感度帯をプロットする：

解の曲面の色を変えることでaとcに対する感度を示す：

パラメータのフィッティング  (2)

微分方程式の解をサンプルとして取り，ノイズを加える：

三角法のモデルをノイズの多いデータにフィットする：

二次モデルの方がよくフィットする：

微分方程式の解がデータに最もよくフィットするパラメータを求める：

データをカルビンに変換し，最初と最後の（アンビエント）温度を求める：

パラメータk1とk2に依存する，ニュートンの冷却法則の解を求める：

微分方程式のパラメータを与えられたデータにフィットする：

特性と関係  (3)

NDSolveValueを使ってパラメータを持つ微分方程式を解く：

指定されたパラメータ値について，各関数の呼出しにはほぼ同じ時間がかかる：

ParametricNDSolveは解をキャッシュし，キャッシュした解の値を再度使う：

DSolveは閉じた形のパラメータを持つ微分方程式を解くことができることもある：

ParametricNDSolveValueを使って例題を数値的に解く：

どちらの方法を使っても感度は等しい：

SystemModelParametricSimulateを使って大きい階層的系のモデルのシミュレーションを行う：

抵抗器とバネ減衰器のパラメータ2セットでシミュセーションを行う：

結果の角速度を比較する：

考えられる問題  (1)

WhenEvent，ReapおよびSowによる解のサンプリングは，各パラメータ値への最初の呼出しにのみ使うことができる：

解がすでにキャッシュされている場合には，値は蒔かれない：

Wolfram Research (2012), ParametricNDSolveValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html （2014年に更新）.

テキスト

Wolfram Research (2012), ParametricNDSolveValue, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html （2014年に更新）.

CMS

Wolfram Language. 2012. "ParametricNDSolveValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html.

APA

Wolfram Language. (2012). ParametricNDSolveValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html

BibTeX

@misc{reference.wolfram_2024_parametricndsolvevalue, author="Wolfram Research", title="{ParametricNDSolveValue}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parametricndsolvevalue, organization={Wolfram Research}, title={ParametricNDSolveValue}, year={2014}, url={https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html}, note=[Accessed: 14-November-2024 ]}