ParametricNDSolveValue
ParametricNDSolveValue[eqns,expr,{x,xmin,xmax},pars]
给出由常微分方程 eqns 的数值解决定的函数的 expr 值,其中自变量 x 位于从 xmin 到 xmax 的范围内,参数为 pars.
ParametricNDSolveValue[eqns,expr,{x,xmin,xmax},{y,ymin,ymax},pars]
在矩形区域上求解偏微分方程 eqns.
ParametricNDSolveValue[eqns,expr,{x,y}∈Ω,pars]
在区域 Ω 上求解偏微分方程 eqns.
ParametricNDSolveValue[eqns,expr,{t,tmin,tmax},{x,y}∈Ω,pars]
在区域 Ω 上求解时间相关偏微分方程 eqns.
更多信息和选项


- ParametricNDSolveValue 给出具有 ParametricFunction 对象的结果.
- {pspec1,pspec2,…} 的参数 pars 的规范可用于指定范围.
- pspeci 的可能形式为:
-
p p 值为 Reals 或 Complexes Element[p,Reals] p 值为 Reals Element[p,Complexes] p 值为 Complexes Element[p,{v1,…}] p 具有离散值 {v1,…} {p,pmin,pmax} p 值为 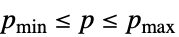
- 通常 expr 会通过微分方程组的解间接与参数相关,但是可能显式与参数相关.
- 由此得出关于参数的 ParametricFunction 对象的导数会尽可能地组合使用符号和数值灵敏度方法进行计算.
- ParametricNDSolveValue 接受与 NDSolve 同样的选项和设置.
- NDSolve 和 ParametricNDSolveValue 通常通过多个不同的阶段求解微分方程组. 当 Method->{s1->m1,s2->m2,…} 时,阶段 si 由方法 mi 处理. 基于所要解决的问题,实际使用的阶段和顺序是由 NDSolve 决定的.
- 可能的解阶段与 NDSolve 是一样的,但还包括:
-
"ParametricCaching" 缓存计算的解 "ParametricSensitivity" 关于参数导数的计算
所有选项的列表

范例
打开所有单元关闭所有单元基本范例 (3)
使用 FindRoot 函数求根:
范围 (6)
参数相关 (4)
ParametricNDSolveValue 返回一个 ParametricFunction 对象:
推广和延伸 (2)
求各种 WorkingPrecision 值的 ![]() 且
且 ![]() 的解,并绘制误差:
的解,并绘制误差:
考虑求出 NDSolveValue 无法直接求解的高度非线性问题的解. 设置边界条件、区域和依赖于参数 ![]() 的方程:
的方程:
NDSolveValue 无法求解:
基于参数 ![]() 创建 ParametricNDSolveValue 函数:
创建 ParametricNDSolveValue 函数:
选项 (2)
应用 (14)
属性和关系 (3)
使用 NDSolveValue 求解带有参数的微分方程:
ParametricNDSolve 缓存解并接着重新使用缓存的解的值:
DSolve 可以解析式求解带有参数的某些微分方程:
使用 ParametricNDSolveValue 数值求解范例:
使用 SystemModelParametricSimulate 模拟更大的分层系统模型:
文本
Wolfram Research (2012),ParametricNDSolveValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "ParametricNDSolveValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html.
APA
Wolfram 语言. (2012). ParametricNDSolveValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ParametricNDSolveValue.html 年