PeanoCurve

PeanoCurve[n]

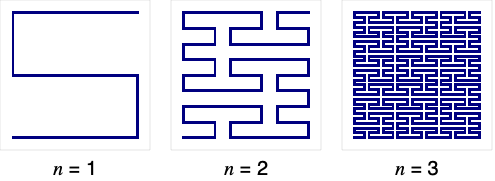
ステップ n のペアノ曲線を表す線分を与える．

詳細とオプション

  • PeanoCurveはペアノ(Peano)空間充填曲線としても知られている．
  • PeanoCurveは，(3n-1) x (3n-1)の正方形上の{0,0}から{3n-1,3n-1}までのすべての整数点を繋ぐ経路に相当するLineプリミティブを返す． »
  • PeanoCurveは，座標が占めるであろうと考えられる範囲の指定に使うことができるDataRangeオプションを取る．

例題

すべて開くすべて閉じる

例  (2)

2Dペアノ曲線：

ペアノ曲線の近似長：

式は以下のようになる：

2Dのペアノ曲線をスプライン曲線で可視化する：

スコープ  (6)

曲線指定  (2)

2Dペアノ曲線：

ベアノ曲線の n 番目の近似：

曲線のスタイル  (4)

太さの異なるペアノ曲線：

スケールされたサイズによる太さ：

印刷用ポイント数による太さ：

破線曲線：

色付きの曲線：

オプション  (1)

DataRange  (1)

DataRangeを使うと生成するメッシュ座標の範囲を指定することができる：

別の範囲を指定する：

アプリケーション  (4)

PeanoCurveは，線分を直線で繋いだ曲線に繰り返し変換することで構築される：

次の反復：

ペアノ曲線を2Dで可視化する：

スプライン曲線を使って可視化する：

単純な多角形を作る：

ペアノ曲線のテクスチャを曲面に適用する：

特性と関係  (3)

PeanoCurveは直線からなる：

2Dペアノ曲線の長さを求める：

DataRange->range はRescalingTransform[{...},range]を使うことに等しい：

RescalingTransformを使う：

考えられる問題  (2)

デフォルトで，ペアノ曲線の座標は単位正方形内にはない：

DataRangeを使って単位正方形内のペアノ曲線を生成する：

PeanoCurveが大きすぎて生成できないことがある：

おもしろい例題  (1)

走査アニメーション：

Wolfram Research (2017), PeanoCurve, Wolfram言語関数， https://reference.wolfram.com/language/ref/PeanoCurve.html.

テキスト

Wolfram Research (2017), PeanoCurve, Wolfram言語関数， https://reference.wolfram.com/language/ref/PeanoCurve.html.

CMS

Wolfram Language. 2017. "PeanoCurve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PeanoCurve.html.

APA

Wolfram Language. (2017). PeanoCurve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PeanoCurve.html

BibTeX

@misc{reference.wolfram_2024_peanocurve, author="Wolfram Research", title="{PeanoCurve}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/PeanoCurve.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_peanocurve, organization={Wolfram Research}, title={PeanoCurve}, year={2017}, url={https://reference.wolfram.com/language/ref/PeanoCurve.html}, note=[Accessed: 21-November-2024 ]}