PeanoCurve
PeanoCurve[n]
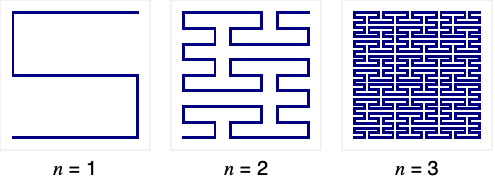
给出表示第 n![]() -步皮亚诺曲线的线段.
-步皮亚诺曲线的线段.
更多信息和选项

- PeanoCurve 也被称作皮亚诺空间填充曲线.
- PeanoCurve 返回的 Line 基元对应的路径由 {0,0} 开始,然后连接 3n-1 乘 3n-1 正方形的所有整数点,并在 {3n-1,3n-1} 结束. »
- PeanoCurve 接受 DataRange 选项,可用于指定坐标应该占据的范围.
范例
打开所有单元关闭所有单元选项 (1)
DataRange (1)
DataRange 允许您指定要生成的网格坐标的范围:
应用 (4)
属性和关系 (3)
PeanoCurve 由线做成组成:
DataRange->range 等效于使用 RescalingTransform[{...},range]:
可能存在的问题 (2)
Wolfram Research (2017),PeanoCurve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PeanoCurve.html.
文本
Wolfram Research (2017),PeanoCurve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PeanoCurve.html.
CMS
Wolfram 语言. 2017. "PeanoCurve." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PeanoCurve.html.
APA
Wolfram 语言. (2017). PeanoCurve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PeanoCurve.html 年