RiccatiSolve

RiccatiSolve[{a,b},{q,r}]

連続代数リッカティ(Riccati)方程式 TemplateBox[{a}, ConjugateTranspose].x+x.a-x.b.TemplateBox[{r}, Inverse].TemplateBox[{b}, ConjugateTranspose].x+q=0の安定化解である行列 を与える．

RiccatiSolve[{a,b},{q,r,p}]

方程式 TemplateBox[{a}, ConjugateTranspose].x+x.a-(x.b+p).TemplateBox[{r}, Inverse].(TemplateBox[{b}, ConjugateTranspose].x+TemplateBox[{p}, ConjugateTranspose])+q=0を解く．

詳細とオプション

  • TemplateBox[{a}, ConjugateTranspose].x+x.a-x.b.TemplateBox[{r}, Inverse].TemplateBox[{b}, ConjugateTranspose].x+q=0の「」は共役転置を示す．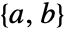
  • が安定化可能で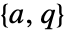が検出可能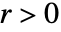，で のとき，方程式 TemplateBox[{a}, ConjugateTranspose].x+x.a-x.b.TemplateBox[{r}, Inverse].TemplateBox[{b}, ConjugateTranspose].x+q=0には一意的で対称な半正定値解 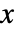がある．これにより，行列 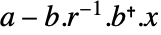の固有値はすべて負で解は安定化される．
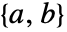  • が可制御で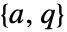が可観測のとき，解は正定値である．
  • RiccatiSolveはMethodオプションをサポートする．以下は，その可能な設定値である．
  • Automatic自動的に決定されたメソッド
    "Eigensystem"固有値分解に基づく
    "GeneralizedEigensystem"一般化された固有値分解に基づく
    "GeneralizedSchur"一般化されたSchur分解に基づく
    "InverseFree""GeneralizedSchur"の変化形
    "MatrixSign"行列符号関数を使った反復法
    "Newton"反復ニュートン法
    "Schur"Schur分解に基づく
  • メソッドはどれも近似数値行列に適用される．"Eigensystem"は厳密行列にも適用される．

例題

すべて開くすべて閉じる

例  (1)

連続代数リッカティ方程式を解く：

解を確かめる：

スコープ  (3)

連続リッカティ方程式を解く：

状態制御カップリングのリッカティ方程式を解く：

状態空間モデルオブジェクトから適切な行列を抽出することでリッカティ方程式を解く：

オプション  (7)

Method  (7)

Automaticおよび"Eigensystem"メソッドは，厳密な系に使うことができる：

厳密ではない系にも使える：

厳密ではない系には"Schur"法が使われることもある：

"Newtonは厳密ではない系に適用され，Automaticよりも正確であることがある：

解と絶対誤差を計算する：

デフォルトのメソッドと比較する：

"Newton"は，"StartingMatrix"，"MaxIterations"，"Tolerance"のサブオプションを取る：

"Newton"法は，安定化解が存在するときでも収束しないことがある：

Automaticメソッドと比較する：

"MatrixSign"は，一般に，"Newton"法の初期近似に使われる：

xinit を使って"Newton"法を初期化する：

誤差を比較する：

"MatrixSign"は，"MaxIterations"および"Tolerance"のサブオプションを取る：

"GeneralizedSchur"および"GeneralizedEigensystem"は，a が特異値の場合に適用される：

行列 a は特異行列である：

これらの2つのメソッドは，特異値 a に使うことができる：

誤差を確かめる：

"InverseFree"は r の条件がよくない場合に使うことができる：

行列 r の条件番号は高い：

このメソッドを使う：

デフォルトのメソッドと比較する：

絶対誤差は，この場合はデフォルトメソッドの方が高い：

アプリケーション  (3)

線形化された倒立振子の最適軌道に関連した費用を計算する：

最適費用は.x.sinitである：

数値積分で費用を求める：

最適軌道に沿って各値についての「cost-to-go（かかる費用）」を追跡する：

すべての閉ループ極を の左側に置く最適化状態フィードバックゲインを計算する：

規定の安定度を持たない閉ループ極：

Kalman推定器の最小誤差共分散を計算する：

特性と関係  (8)

クロスカップリング行列 p で最適ゲインを求める：

p を行列 a および q に組み込むことによっても同様の結果が求まる：

{a,b}が可制御，{a,g}が可観測であり q=Transpose[g].g であれば，リッカティ方程式の解は正定値である：

ハミルトン行列 の固有値は{λ,-λ}の形式のペアである：

と は相似行列である：

安定化解が求まるかどうかはハミルトン行列にかかっている：

ハミルトン行列は安定性特性を満たさなければならない：

同時に相補性特性も満たさなければならない：

安定化解：

のフィードバック系の固有値を求める：

これらはハミルトン行列の安定固有値でもある：

RiccatiSolveを使って最適化状態フィードバックゲインを計算する：

LQRegulatorGainsを使って同じ結果を直接計算する：

RiccatiSolveを使って最適化出力フィードバックゲインを計算する：

LQOutputRegulatorGainsも同じ結果を与える：

RiccatiSolveを使って最適化推定器ゲインを計算する：

LQEstimatorGainsを使ってこの結果を直接計算する：

考えられる問題  (1)

が安定化不可能であるか，が検出不可能な場合，q=TemplateBox[{g}, Transpose].g のリッカティ方程式には安定化解がない：

Wolfram Research (2010), RiccatiSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiccatiSolve.html （2014年に更新）.

テキスト

Wolfram Research (2010), RiccatiSolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiccatiSolve.html （2014年に更新）.

CMS

Wolfram Language. 2010. "RiccatiSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/RiccatiSolve.html.

APA

Wolfram Language. (2010). RiccatiSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiccatiSolve.html

BibTeX

@misc{reference.wolfram_2024_riccatisolve, author="Wolfram Research", title="{RiccatiSolve}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RiccatiSolve.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riccatisolve, organization={Wolfram Research}, title={RiccatiSolve}, year={2014}, url={https://reference.wolfram.com/language/ref/RiccatiSolve.html}, note=[Accessed: 21-November-2024 ]}