SymmetricReduction
SymmetricReduction[f,{x1,…,xn}]
gives a pair of polynomials ![]() in
in ![]() such that
such that ![]() , where
, where ![]() is the symmetric part and
is the symmetric part and ![]() is the remainder.
is the remainder.
SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]
gives the pair ![]() with the elementary symmetric polynomials in
with the elementary symmetric polynomials in ![]() replaced by
replaced by ![]() .
.
Details

- If
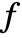 is a symmetric polynomial, then
is a symmetric polynomial, then 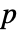 is the unique polynomial in elementary symmetric polynomials equal to
is the unique polynomial in elementary symmetric polynomials equal to 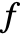 , and
, and 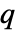 is zero.
is zero. - If
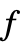 is not a symmetric polynomial, then the output
is not a symmetric polynomial, then the output 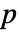 is not unique, but depends on the ordering of its variables.
is not unique, but depends on the ordering of its variables. - For a given ordering, a nonsymmetric polynomial
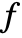 can be expressed uniquely as a sum of its symmetric part
can be expressed uniquely as a sum of its symmetric part 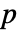 and a remainder
and a remainder 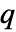 that does not contain descending monomials. A monomial
that does not contain descending monomials. A monomial 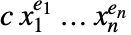 is called descending if
is called descending if  .
. - Changing the ordering of the variables may produce different pairs
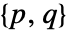 .
. - SymmetricReduction does not check to see that
 is a polynomial, and will attempt to symmetrize the polynomial part of
is a polynomial, and will attempt to symmetrize the polynomial part of 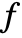 .
.
Examples
open allclose allBasic Examples (3)
Scope (2)
SymmetricReduction will reduce the polynomial part of an expression:
Applications (2)
Let the roots of the equation ![]() be
be ![]() ,
, ![]() ,
, ![]() . The coefficients
. The coefficients ![]() ,
, ![]() ,
, ![]() are trivially related to the symmetric polynomials of
are trivially related to the symmetric polynomials of ![]() ,
, ![]() ,
, ![]() :
:
A similar expression holds for the monic polynomial with roots ![]() ,
, ![]() ,
, ![]() :
:
Use SymmetricReduction to solve for ![]() ,
, ![]() ,
, ![]() :
:
The monic polynomial with roots ![]() ,
, ![]() ,
, ![]() :
:
Consider solving the following symmetric system of equations:
Use ChebyshevT to convert to a symmetric system of polynomials:
Solve is able to solve the equations in the variables x1,x2,x3:
The leaf count of the solution is enormous:
Convert to a system of equations of symmetric polynomials ![]() :
:
Solve the new system of equations:
The leaf count of the symmetric solution is much smaller:
Solving for the variables x1,x2,x3 in terms of the symmetric polynomials ![]() is also quick:
is also quick:
Properties & Relations (2)
The order of variables can affect the decomposition into symmetric and nonsymmetric parts:
Another basis for the symmetric polynomials consists of the complete symmetric polynomials. They are the sum of all monomials of a given degree, and can be defined by the generating function Product[1-xit,{i,n}]-1:
A determinant formula expresses the elementary symmetric polynomials in the basis of the complete symmetric polynomials:
Any symmetric polynomial can also be expressed in terms of the complete symmetric polynomials:
Text
Wolfram Research (2007), SymmetricReduction, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricReduction.html.
CMS
Wolfram Language. 2007. "SymmetricReduction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricReduction.html.
APA
Wolfram Language. (2007). SymmetricReduction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricReduction.html