WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

Wolfram言語＆システムドキュメントセンター

SymmetricReduction

SymmetricReduction

SymmetricReduction[f,{x₁,…,x_n}]

においてであるような多項式のペアを与える．ただし，は対称な部分でありは剰余である．

SymmetricReduction[f,{x₁,…,x_n},{s₁,…,s_n}]

における初等対称式をで置き換えたペアを与える．

詳細

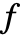が対称多項式であるなら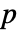，は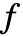と同値である初等対称多項式の中の一意的な多項式であり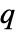，は0である．
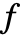が対称多項式ではなければ，出力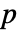は一意的ではなく，その変数の順序に依存する．
任意の順序において，対称ではない多項式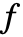は，対称な部分の和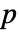と下向きの単項式を含まない剰余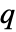として一意的に表すことができる．単項式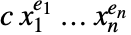は，であれば下向きと呼ばれる．
変数の順序を変えると異なるペア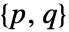が生ずることがある．
SymmetricReductionは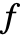，が多項式であるかどうか判定せず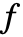，の多項式部分を対称化しようとする．

例題

すべて開くすべて閉じる

例 (3)

初等対称多項式の和として対称多項式を書く：

剰余の対称部分と剰余として非対称多項式を書く：

最初の2つの初等対称多項式をs1とs2を指定する：

スコープ (2)

SymmetricReductionは，式の対称部分を簡約する：

アプリケーション (2)

方程式の根が , , であるとする．係数 , , は , , の対称多項式と自明に関係している：

同様の方程式は根, , を持つ単多項式にも当てはまる：

SymmetricReductionを使って, , について解く：

根 , , を持つ単多項式：

チェックする：

次の対称方程式系を解いてみよう：

ChebyshevTを使って対称な多項式系に変換する：

Solveは，変数x₁,x₂,x₃中の方程式を解くことができる：

解における「葉」の数は莫大である：

対称多項式の方程式系に変換する：

新たな方程式系を解く：

対称解における「葉」の数はすっと少ない：

変数x₁,x₂,x₃について対称多項式を解くのも同じように速い：

特性と関係 (2)

変数の順序が対称な部分と非対称な部分への分解に影響することがある：

対称多項式のもう1つの原則は完全な対称多項式からなっている．これらは任意の次数のすべての単項式の和で，母関数Product[1-x_it,{i,n}]^-1で定義することができる：

行列式は完全な対称多項式に基づいた初等対称多項式を表している：

チェックする：

完全な対称多項式に基づいて任意の対称多項式を表すこともできる：

Top