WOLFRAM

Wolfram 语言与系统参考资料中心

SymmetricReduction[f,{x1,…,xn}]

给出一对关于 的多项式 ，使得 ，其中 为对称部分， 为余部.

SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]

用 表示 中的对称多项式 .

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
应用  
属性和关系  
参见
技术笔记
相关指南
历史
按以下格式引用：

SymmetricReduction

SymmetricReduction[f,{x1,…,xn}]

给出一对关于 的多项式 ，使得 ，其中 为对称部分， 为余部.

SymmetricReduction[f,{x1,…,xn},{s1,…,sn}]

用 表示 中的对称多项式 .

更多信息

  • 若 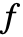f 为对称多项式，那么 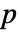是基本对称多项式中唯一等于 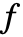f 的多项式，而 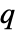为零.
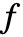  • 若 f 不是对称多项式，那么输出 并不唯一，取决于变量的次序.
  • 在给定的次序下，一个非对称多项式 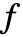f 可唯一表达为对称多项式 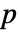和不含降幂单项式的余部 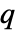的和. 若 ，单项式 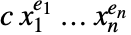称为降幂单项式.
  • 交换项的次序可能会得到不同的 .
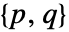  • SymmetricReduction 不会检查 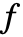f 是否是一个多项式，而会试图对称化 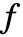f 的多项式部分.

范例

打开所有单元 关闭所有单元

基本范例  (3)

将对称多项式分解为基本对称多项式的和：

Wolfram Language code: SymmetricReduction[x ^ 2 + y ^ 2, {x, y}]

将非对称多项式分解为对称部分和余部：

Wolfram Language code: SymmetricReduction[x ^ 2 - y ^ 2, {x, y}]

将前两个基本对称多项式命名为 s1 和 s2：

Wolfram Language code: SymmetricReduction[x ^ 2 - y ^ 2, {x, y}, {s1, s2}]

范围  (3)

对于对称多项式，结果与变量的顺序无关：

Wolfram Language code: SymmetricReduction[x ^ 5 + 2x y ^ 2 + 2y x ^ 2 + y ^ 5, {x, y}, {s1, s2}]
Wolfram Language code: SymmetricReduction[x ^ 5 + 2x y ^ 2 + 2y x ^ 2 + y ^ 5, {y, x}, {s1, s2}]

对于非对称多项式，结果取决于变量的顺序：

Wolfram Language code: SymmetricReduction[x ^ 3 - 3x y ^ 2 + y ^ 5, {x, y}, {s1, s2}]
Wolfram Language code: SymmetricReduction[x ^ 3 - 3x y ^ 2 + y ^ 5, {y, x}, {s1, s2}]

SymmetricReduction 会化简表达式的多项式部分：

Wolfram Language code: SymmetricReduction[x y + Sin[x y + x z + y z], {x, y, z}, {s1, s2, s3}]

应用  (2)

方程 的根为 , , . 系数 , , 取决于 , , 的对称多项式：

Wolfram Language code: poly1 = x^3 + a x^2 + b x + c;
Wolfram Language code: SolveAlways[poly1 == (x - α)(x - β)(x - γ), x]
Wolfram Language code: SymmetricPolynomial[#, {α, β, γ}]& /@ Range[3]

类似的表达式对于根为 、、 的首一多项式成立：

Wolfram Language code: SolveAlways[x^3 + Overscript[a, _]x^2 + Overscript[b, _]x + Overscript[c, _] == (x - α^2)(x - β^2)(x - γ^2), x]

用 SymmetricReduction 求出 , , ：

Wolfram Language code: {Overscript[a, _], Overscript[b, _], Overscript[c, _]} = Part[SymmetricReduction[#, {α, β, γ}, {-a, b, -c}]& /@ {-α^2 - β^2 - γ^2, α^2β^2 + α^2γ^2 + β^2γ^2, -α^2β^2γ^2}, All, 1]

根为 、、 的首一多项式：

Wolfram Language code: poly2 = x^3 + Overscript[a, _]x^2 + Overscript[b, _]x + Overscript[c, _]

检验：

Wolfram Language code: x^2 /. NSolve[poly1 /. {a -> 3, b -> 5, c -> 7}, x]//Sort
Wolfram Language code: x /. NSolve[poly2 /. {a -> 3, b -> 5, c -> 7}, x]//Sort

考虑求解如下对称多项式组：

Wolfram Language code: system = { Cos[Subscript[a, 1]] + Cos[Subscript[a, 2]] + Cos[Subscript[a, 3]] - k == 0, Cos[5Subscript[a, 1]] + Cos[5Subscript[a, 2]] + Cos[5Subscript[a, 3]] == 0, Cos[7Subscript[a, 1]] + Cos[7Subscript[a, 2]] + Cos[7Subscript[a, 3]] == 0 };

用 ChebyshevT 转换对称多项式组：

Wolfram Language code: eqns = system /. Cos[n_.Subscript[a, i_]] :> ChebyshevT[n, Subscript[x, i]]

Solve 可以求解变量为 x1,x2,x3 的方程：

Wolfram Language code: SetOptions[Solve, Cubics -> False, Quartics -> False];
Wolfram Language code: r1 = Solve[eqns, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}];//Timing

解决方案叶子数量很多：

Wolfram Language code: LeafCount[r1]

转换为 的对称多项式组成的方程组：

Wolfram Language code: symeqns = Map[SymmetricReduction[#, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, {Subscript[e, 1], Subscript[e, 2], Subscript[e, 3]}][[1]]&, eqns, {2}]

求解新的方程组：

Wolfram Language code: r2 = Solve[symeqns, {Subscript[e, 1], Subscript[e, 2], Subscript[e, 3]}];//Timing

对称解决方案的叶子数量明显下降：

Wolfram Language code: LeafCount[r2]

关于对称多项式 求解变量 x1,x2,x3 耗时很短：

Wolfram Language code: Solve[Table[SymmetricPolynomial[k, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}] == Subscript[e, k], {k, 3}], {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}];//Timing

属性和关系  (2)

变量的顺序会影响对称部分和非对称部分的分解：

Wolfram Language code: SymmetricReduction[x ^ 2 - y ^ 2, {x, y}]
Wolfram Language code: SymmetricReduction[x ^ 2 - y ^ 2, {y, x}]

对称多项式的另一基本组成单位是完全对称多项式. 它们是具有给定阶数的所有单项式的和，并且可以使用生成函数 Product[1-xit,{i,n}]-1 定义：

Wolfram Language code: complete = Solve[1 + Subscript[h, 1]t + Subscript[h, 2]t^2 + Subscript[h, 3]t^3 + O[t]^4 == (1/Underoverscript[∏, i = 1, 3](1 - Subscript[x, i]t)) + O[t]^4, {Subscript[h, 1], Subscript[h, 2], Subscript[h, 3]}][[1]]

对称多项式和完全对称多项式之间关系的公式：

Wolfram Language code: {Subscript[e, 1], Subscript[e, 2], Subscript[e, 3]} == {Subscript[h, 1], Det[| | | | -- | -- | | h1 | h2 | | 1 | h1 |], Det[| | | | | -- | -- | -- | | h1 | h2 | h3 | | 1 | h1 | h2 | | 0 | 1 | h1 |]}

检验：

Wolfram Language code: %[[2]] /. complete//Expand
Wolfram Language code: SymmetricPolynomial[#, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}]& /@ Range[3]

任何对称多项式也可以关于完全对称多项式表示：

Wolfram Language code: SymmetricReduction[x y z(x + y)(x + z)(y + z), {x, y, z}, {Subscript[e, 1], Subscript[e, 2], Subscript[e, 3]}] /. {Subscript[e, 1] -> Subscript[h, 1], Subscript[e, 2] -> Det[| | | | -- | -- | | h1 | h2 | | 1 | h1 |], Subscript[e, 3] -> Det[| | | | | -- | -- | -- | | h1 | h2 | h3 | | 1 | h1 | h2 | | 0 | 1 | h1 |]}//Expand
Wolfram Research (2007)，SymmetricReduction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SymmetricReduction.html.

文本

Wolfram Research (2007)，SymmetricReduction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SymmetricReduction.html.

CMS

Wolfram 语言. 2007. "SymmetricReduction." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SymmetricReduction.html.

APA

Wolfram 语言. (2007). SymmetricReduction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SymmetricReduction.html 年

BibTeX

@misc{reference.wolfram_2026_symmetricreduction, author="Wolfram Research", title="{SymmetricReduction}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricReduction.html}", note=[Accessed: 05-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_symmetricreduction, organization={Wolfram Research}, title={SymmetricReduction}, year={2007}, url={https://reference.wolfram.com/language/ref/SymmetricReduction.html}, note=[Accessed: 05-November-2026]}