SystemsModelLinearity

SystemsModelLinearity[sys]

系のモデル sys の線形性を与える．

SystemsModelLinearity[{sys,{in1,…},{out1,…},{s1,…}}]

入力 ini，出力 outj，状態 skに関連した部分系のみを考慮する．

詳細

  • SystemsModelLinearityは，一般に，NonlinearStateSpaceModelあるいはAffineStateSpaceModelが，より特化した形への厳密変換を可能とし，したがって適用可能な設計や分析技術の幅が広がる，追加の線形性条件を満足するかどうかの決定に使われる．
  • 可能な系のモデル sys には，TransferFunctionModel，StateSpaceModel，AffineStateSpaceModel，NonlinearStateSpaceModelがある．
  • 状態 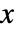，入力 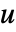，状態方程式 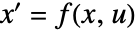，出力方程式 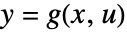の状態空間モデルは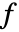， および 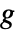内のどの変数が線形に出現するかに基づいて分類される．
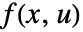  • および 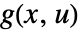の両方に求められる，可能な値と構造的形
  • "Linear"状態と入力が線形，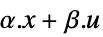
    "Bilinear"状態と入力が別々に線形，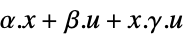
    "StateLinear"状態のみが線形，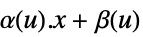
    "InputLinear"入力のみが線形，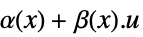
    "Nonlinear"状態も入力も線形ではない

例題

すべて開くすべて閉じる

例  (2)

線形質量バネダンパー(MSD)モデル：

バネが三次非線形性を持つMSDモデル：

スコープ  (7)

線形モデル：

線形のNonlinearStateSpaceModel：

双一次モデル：

入力線形モデル：

線形ではないモデル：

周波数領域モデルは線形モデルである：

線形状態方程式のあるモデル：

アプリケーション  (2)

StateTransformationLinearizeを使って得た線形化を確かめる：

入力出力線形かどうかをチェックする：

状態出力線形かどうかをチェックする：

入力状態線形かどうかをチェックする：

系を繋いだ後で線形化を計算する：

2つの系を直列に接続する：

もとの系と接続された系の線形性：

特性と関係  (4)

線形系は重ね合せと均質性の原則に従う：

入力信号 に対する応答：

TemplateBox[{t}, UnitStepSeq]に対する応答：

3 sin(t)+5 TemplateBox[{t}, UnitStepSeq]に対する応答はと同じである：

一般に，線形の状態空間モデルのモデル化にはStateSpaceModelが使われる：

このモデルは，他の任意の系のモデルに厳密に変換することができる：

一般に，双一次あるいは入力線形のモデルにはAffineStateSpaceModelが使われる：

これは，NonlinearStateSpaceModelに厳密に変換することができる：

他の系のモデルへの変換は近似的になる：

線形ではないモデルにはNonlinearStateSpaceModelを使う：

他の任意の系のモデルへの変換は近似的になる：

Wolfram Research (2014), SystemsModelLinearity, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

テキスト

Wolfram Research (2014), SystemsModelLinearity, Wolfram言語関数， https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

CMS

Wolfram Language. 2014. "SystemsModelLinearity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SystemsModelLinearity.html.

APA

Wolfram Language. (2014). SystemsModelLinearity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SystemsModelLinearity.html

BibTeX

@misc{reference.wolfram_2024_systemsmodellinearity, author="Wolfram Research", title="{SystemsModelLinearity}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SystemsModelLinearity.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_systemsmodellinearity, organization={Wolfram Research}, title={SystemsModelLinearity}, year={2014}, url={https://reference.wolfram.com/language/ref/SystemsModelLinearity.html}, note=[Accessed: 21-November-2024 ]}