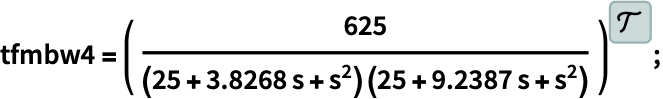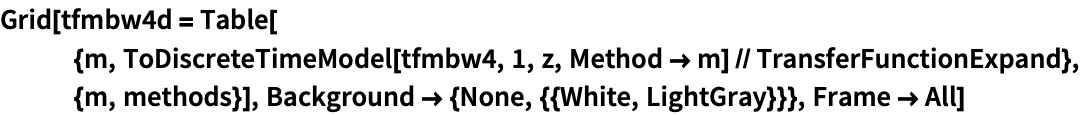WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

ToDiscreteTimeModel
✖
ToDiscreteTimeModel

✖

サンプリング周期が τ の連続時間系モデル lsys の離散時間近似を与える．

✖

変換変数 z を指定する．

詳細とオプション

例題

すべて開くすべて閉じる

例  (1)基本的な使用例

連続時間系の離散時間近似：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-yqjeij
Out[1]=1

スコープ  (6)標準的な使用例のスコープの概要

連続時間伝達関数モデルを離散時間領域に変換する：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-gbj9pt
Out[1]=1

連続時間状態空間モデルを離散時間に変換する：

In[1]:=1
✖
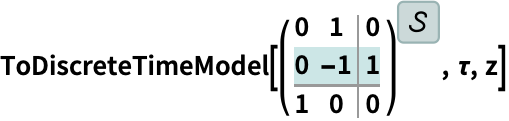
https://wolfram.com/xid/0ixdwwv20qu6bp5-dwvrci
Out[1]=1

多入力多出力(MIMO)系を離散時間に変換する：

In[1]:=1
✖
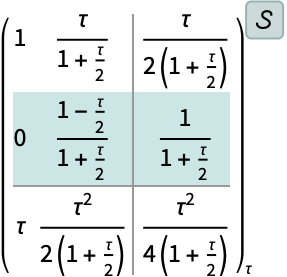
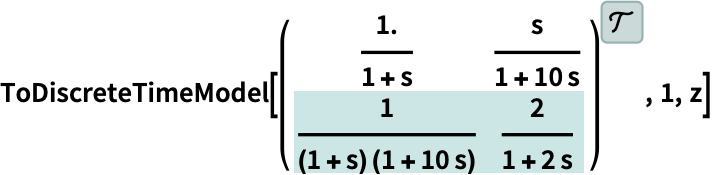
https://wolfram.com/xid/0ixdwwv20qu6bp5-fyhxqh
Out[1]=1

記号による系を変換する：

In[1]:=1
✖
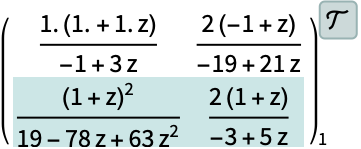
https://wolfram.com/xid/0ixdwwv20qu6bp5-nui2q7
Out[1]=1

時間遅延TransferFunctionModelを変換する：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-hmqzst
Out[1]=1

特異ディスクリプタStateSpaceModelを変換する：

In[1]:=1
✖
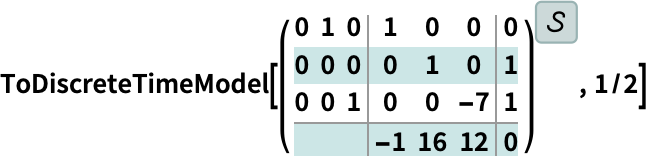
https://wolfram.com/xid/0ixdwwv20qu6bp5-fssn2i
Out[1]=1

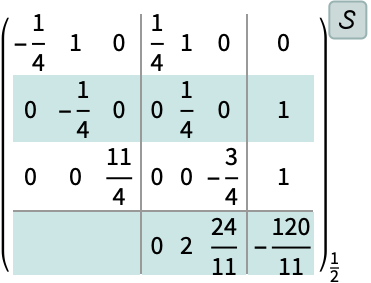
オプション  (5)各オプションの一般的な値と機能

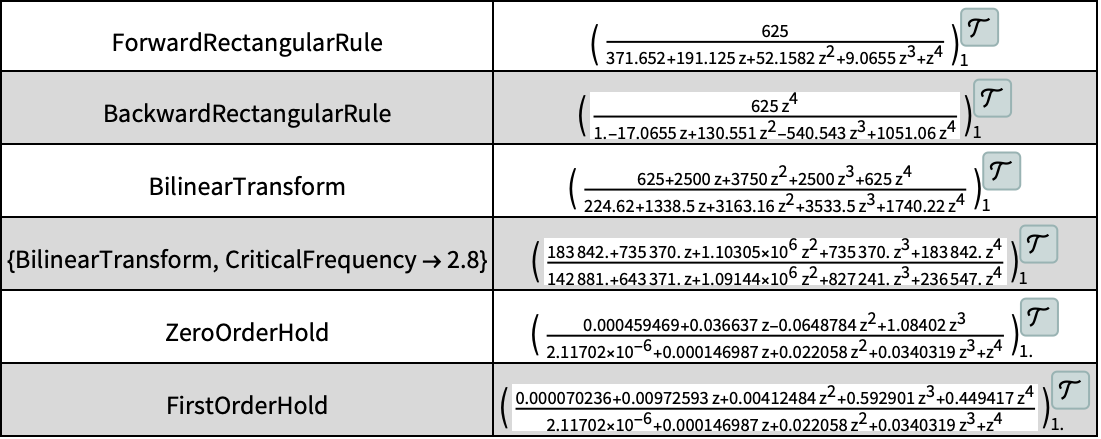
Method  (5)

デフォルトで，近似は双一次変換に基づいて行われる：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-30d01e
Out[1]=1

希望する近似メソッドを指定する：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-bpc2db
Out[1]=1

さまざまな近似メソッドを比較する：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-6obpll
In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-tx549e
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-k7j4m9
Out[3]=3

指定の周波数で伝達を保存する近似：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-vi01iu
In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-31g3l8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-2h0oor
In[4]:=4
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-ylvti7
Out[4]=4

双一次および後退オイラー法はディスクリプタ状態空間モデルに状態を加えることがある：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-nfvh2b
Out[1]=1

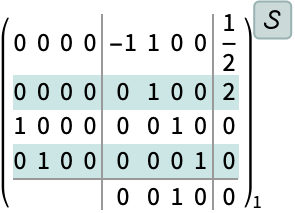
アプリケーション  (1)この関数で解くことのできる問題の例

四次バターワース(Butterworth)ローパスフィルタのさまざまな近似：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-bbt4f5
In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-wajl2s
In[3]:=3
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-nfmlbk
Out[3]=3

ボード線図：

In[4]:=4
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-5pdmw0
Out[4]=4

特性と関係  (5)この関数の特性および他の関数との関係

安定した伝達関数モデル：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-gzcbn8

"ForwardRectangularRule"メソッドは安定した近似を与えないことがある：

In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-wm9hr4
In[3]:=3
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-wdp49t
Out[3]=3

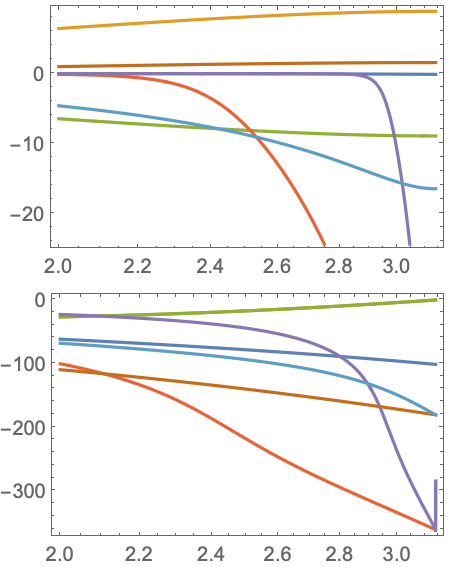
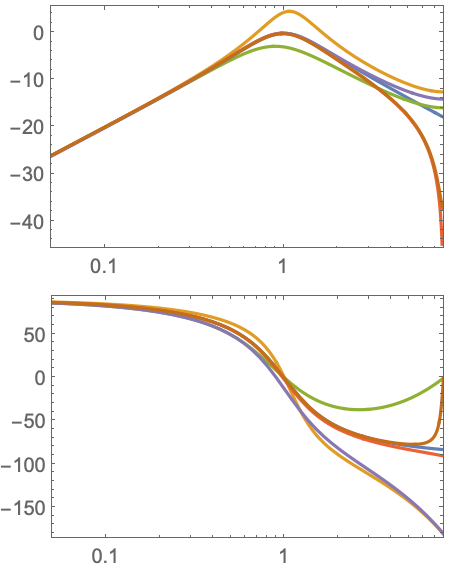
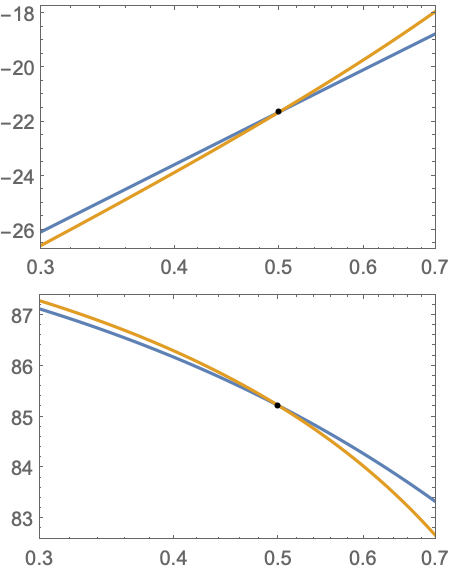
"BilinearTransform"近似の安定性は臨界周波数に依存する：

In[4]:=4
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-btw32b

臨界周波数がナイキスト周波数より少ないと安定した近似が得られる：

In[5]:=5
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-knwy2t
Out[5]=5

臨界周波数がナイキスト周波数より多いと，近似は不安定になる：

In[6]:=6
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-oxxml1
In[7]:=7
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-cwhwt8
Out[7]=7

他のすべての近似は連続時間系が安定していれば安定した系を与える：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-804ddo
In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-h1lvb6
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-8apekz
Out[3]=3

ToContinuousTimeModelは基本的にToDiscreteTimeModelの逆関数である：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-5ak491
In[2]:=2
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-i9fu6d
Out[2]=2

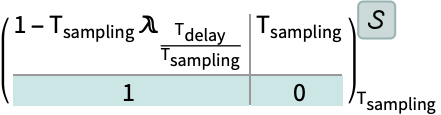
結果の系における遅延はサンプリング周期と相対的に与えられる：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-fv91u5
Out[1]=1

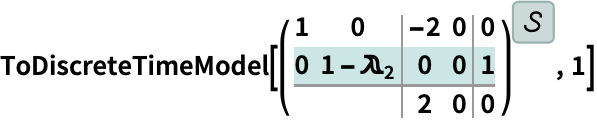
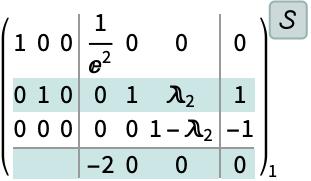
ToDiscreteTimeModelがニュートラル型時間遅延系に状態を加えることがある：

In[1]:=1
✖
https://wolfram.com/xid/0ixdwwv20qu6bp5-m59gtg
Out[1]=1
Wolfram Research (2010), ToDiscreteTimeModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.
✖
Wolfram Research (2010), ToDiscreteTimeModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.

テキスト

Wolfram Research (2010), ToDiscreteTimeModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.

✖
Wolfram Research (2010), ToDiscreteTimeModel, Wolfram言語関数， https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.

CMS

Wolfram Language. 2010. "ToDiscreteTimeModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.

✖
Wolfram Language. 2010. "ToDiscreteTimeModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html.

APA

Wolfram Language. (2010). ToDiscreteTimeModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html

✖
Wolfram Language. (2010). ToDiscreteTimeModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html

BibTeX

@misc{reference.wolfram_2025_todiscretetimemodel, author="Wolfram Research", title="{ToDiscreteTimeModel}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html}", note=[Accessed: 13-April-2025 ]}

✖
@misc{reference.wolfram_2025_todiscretetimemodel, author="Wolfram Research", title="{ToDiscreteTimeModel}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html}", note=[Accessed: 13-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_todiscretetimemodel, organization={Wolfram Research}, title={ToDiscreteTimeModel}, year={2010}, url={https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html}, note=[Accessed: 13-April-2025 ]}

✖
@online{reference.wolfram_2025_todiscretetimemodel, organization={Wolfram Research}, title={ToDiscreteTimeModel}, year={2010}, url={https://reference.wolfram.com/language/ref/ToDiscreteTimeModel.html}, note=[Accessed: 13-April-2025 ]}