TreeGamePayoff
TreeGamePayoff[tgame,strat]
戦略プロファイル strat の木ゲーム tgame における各プレーヤーの期待される利得を与える.
TreeGamePayoff[tgame,strat,adv]
不完全戦略プロファイル strat で敵対するタイプ adv の木ゲーム tgame における各プレーヤーの期待される利得を与える.
詳細

- TreeGamePayoffは,逐次ゲームの期待される利得あるいは期待される効用としても知られている.
- TreeGamePayoffは,一般に,各プレーヤーの戦略が与えられたときにプレーヤーの期待される利得を評価するために使われる.
- 木ゲーム戦略<…,playeri<{ni,1}pri,1,…,{ni,mi}pri,mi>,…>は,playeriについて,行動ノード ni,jにおける playeriの行動確率 pri,jを指定する.
- 選択肢が mj個ある場合の行動ノード njにおけるプレーヤー i の期待される利得 piは pi[{nj}]=
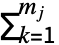 pi[{nj,k}].prj,kで与えられる.ただし,終端ノード ntにおけるプレーヤー i の期待される利得 piは指定された利得で与えられる.すなわち pi[{nt}]=pi,jである.
pi[{nj,k}].prj,kで与えられる.ただし,終端ノード ntにおけるプレーヤー i の期待される利得 piは指定された利得で与えられる.すなわち pi[{nt}]=pi,jである. - 不完全な木戦略は,行動ノードの部分集合にしか確率が指定されていない木ゲームの戦略である.
- 不完全な戦略の場合,未指定の行動 adv に対して以下の指定が与えられる.
-
"Perfect" 未指定の行動に対する最適選択を仮定したランダム試行の利得 "PerfectExpectation" 未指定の行動に対する最適ランダム選択を仮定した平均利得 "Random" 未指定の行動に対する一様ランダム選択を仮定したランダム試行の利得 "RandomExpectation" 未指定の行動に対する一様ランダム選択を仮定した平均利得
例題
すべて開くすべて閉じる例 (3)
スコープ (3)
アプリケーション (5)
社会ゲーム (3)
ムカデゲームでは2人のプレーヤーが交互に意思決定する.プレーヤーは,それぞれの番に「下」に行ってゲームを終了するか「横」に行ってゲームを継続するかが決定できる(最終ノードは例外で「横」に行ってもゲームは終了する).ゲームが長く続けば続くほど総効用は高くなる. 最初にゲームを終了したプレーヤーがその時点の効用の分前をたくさん取得する.各プレーヤーの行動が3種類のムカデゲームについて考える:
ゲームの理論的に最良の解は悲観的な最初の選択であるが,ランダムなプレーヤーの期待利得もそれ似ている点に注意する必要がある.ランダムで完全なプレーヤーの期待される結果を比較する:
硬貨合せの木ゲームは,2人のプレーヤーが互いに硬貨の表と裏を選ぶゲームである.選択したものが違う場合は ,プレーヤー1がプレーヤー2に1ドル支払う.選択が同じ場合はプレーヤー2がプレーヤー1に1ドル支払う.硬貨合せゲームの木ゲームを生成する:
明らかに,このゲームはプレーヤー2が有利で,完全なプレーヤーを相手によりよい利得を取得するのは不可能である.プレーヤー1になった場合を想像してみる.いくつかの戦略を使って完全なプレーヤーに勝つ(利得1を獲得する):
参入ゲームでは,参入者が市場に参入するかどうかを決定し,新規参入者がある場合に既に参入している側がこれと戦うかあるいはこれを受け入れるかを決める.参入ゲームを生成する:
自分が既存の参入者で戦略は常に戦うこと(第1選択)であると考えてみる.ランダムなプレーヤーに対するときの期待される利得を求める:
完全なプレーヤーは完全な部分ゲーム均衡を仮定する.この戦略は部分最適なので,完全なプレーヤーの利得がランダムなプレーヤーのそれよりも悪くなる可能性がある.完全なプレーヤーに対して期待される利得を求める:
娯楽ゲーム (2)
ジャンケンは,一人のプレーヤーが勝って残りのプレーヤーが負けるか引き分けるかのゼロ和ゲームである.最初のプレーヤーの行動を考慮して2番目のプレーヤーが行動を選択できる,このゲームの木ゲームバージョンを生成する:
明らかに,ジャンケンの木ゲームでは,2番目のプレーヤーが常に最適行動を選択でき,したがって最初のプレーヤーは最初に行動するがゆえに不利になる.ジャンケンのこのバージョンの完全戦略を書く:
三目並べのゲームについて考える.プレーヤーAとプレーヤーBの間の部分的な三目並べを生成する関数を設計する:
これに基づいてTreeGame を形成する:
テキスト
Wolfram Research (2025), TreeGamePayoff, Wolfram言語関数, https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
CMS
Wolfram Language. 2025. "TreeGamePayoff." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
APA
Wolfram Language. (2025). TreeGamePayoff. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeGamePayoff.html