TreeGame
TreeGame[{player1,action1,…,actionk}]
specifies an action node for player1 with possible actions actionj.
Details and Options
- TreeGame is also known as extensive form game, sequential move game or game tree.
- A tree game is described as a tree with action nodes where players have a finite number of actions to take and end nodes where the game is over with a resulting payoff for each player. There can be finitely many players taking turns, resulting in a finite game tree.
- TreeGame is typically used to model decision problems with two or more players acting sequentially. Examples include card and board games, but also economic or business games such as market entry, labor negotiations or oligopoly market actions.
- Possible actions actionj include:
-
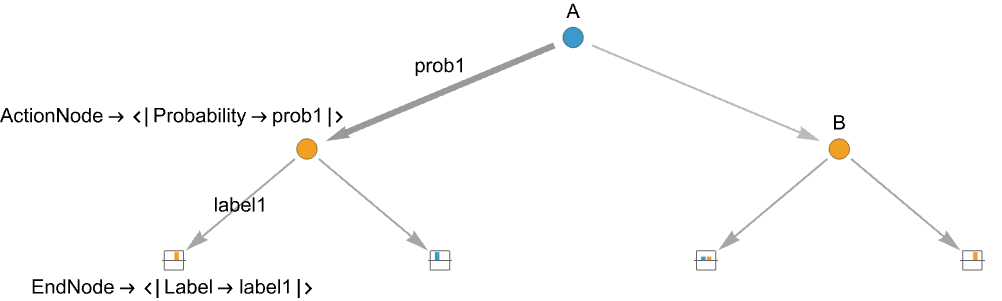
{playerj,action1,…,actionm} an action node where playerj has m possible actions actionj {payoff1,…,payoffn} an end node with payoffs payoffk for the n players - Additional information for action nodes include action labels and action probabilities:
-
{playerj,…,actionilabeli,…} using labeli for actioni {playerj,…,actioniprobi,…} choosing actioni with probability probi {playerj,…,actioni{labeli,probi},…} specify both label and probability - When using probabilistic actions at an action node, then all actions need to have probabilities for that action node.
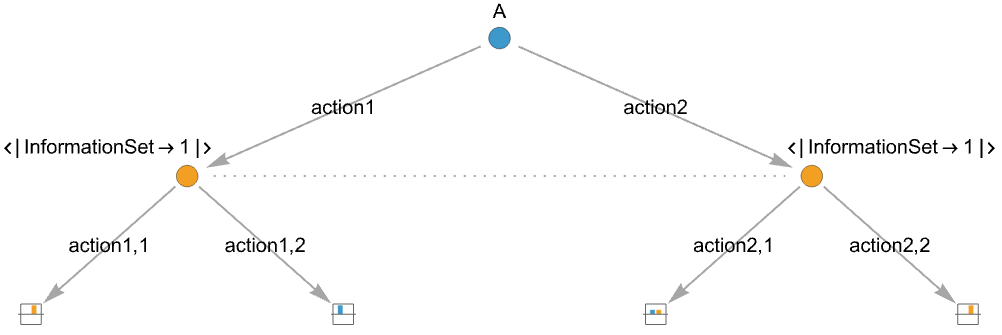
- To model players having imperfect information about which node they are in, the concept of information set is used, which is a label attached to all the action nodes in the same set:
-
{playerjilabelk,action1,…,actionm} using ilabelk for an action node - The possible information sets need to be at the same level in the game tree.
- A typical example of imperfect information is in a card game where you do not know the cards of all the players and hence you do not know which node you are in.
- Using the alternative Tree notation, an action tree may have two forms:
-
Tree[<"Player"playerj>,{actiont1,…,actiontk}] an action node where playerj has m possible actions actionj Tree[<"Payoffs"{payoff1,…,payoffn}>,{}] an end node with payoffs payoffk for the n players - Additional information for action nodes and end nodes includes action labels and action probabilities that refer to the incoming edge:
-
"Label"label - use label for the parent action edge
"Probability"prob specify the probability prob for the parent edge - When using probabilistic actions at an action node, then all actions need to have probabilities for that action node.
- Imperfect information can be indicated in action nodes:
-
"InformationSet"ilab specify the information set of the action tree actionti - If different players use the same information set, they will treated as different information sets.
- If the same player has nodes in the same information set but with a different number of actions, they will be treated as different information sets.
- For a TreeGame g, the following properties "prop" can be accessed as g["prop"]:
-
"Graph" Graph represention of the game "InformationSets" dictonaries of the information sets and the node included "MatrixGame" convert a tree game to a matrix game "PayoffArray" a vector of all payoff values in the game "Players" list of players "Plot" represent the game as a tree plot; see TreeGamePlot "Rules" a Rule representation of the game "Summary" basic data for the game "Tree" a Tree representation of the game "Validity" validation of the tree game - TreeGame can be used in functions such as TreeGamePlot, FindTreeGameStrategies, VerifyTreeGameStrategy and TreeGamePayoff.
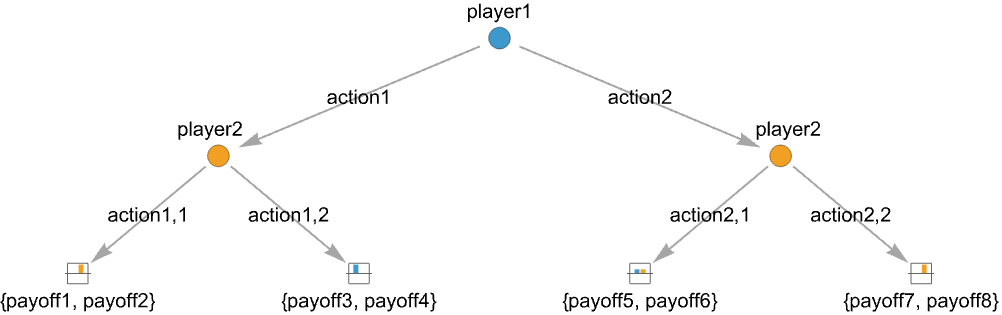
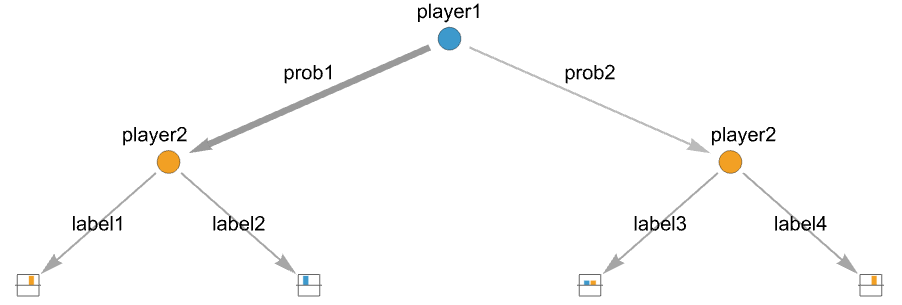
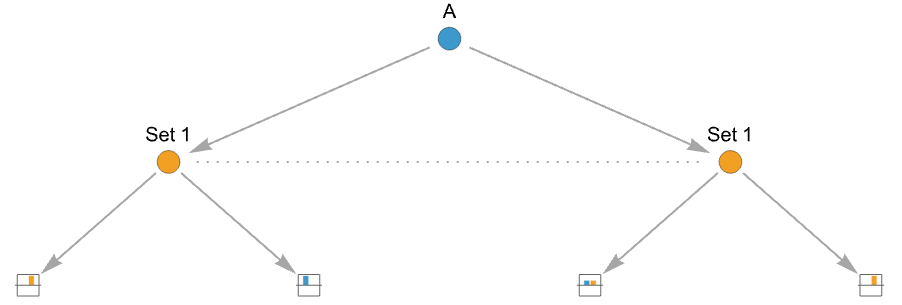
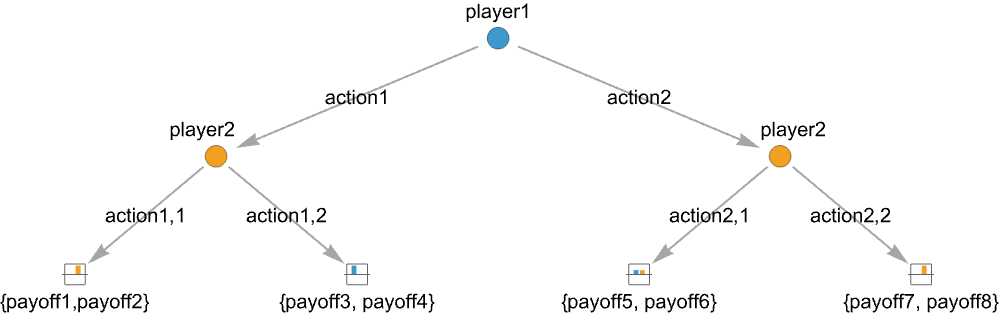
Examples
open allclose allBasic Examples (5)
Create a two-player game where all actions have a probability:
Create a three-player game using trees:
Create a three-player game where each player only has one action:
Each of their actions is part of the same information set:
Create a two-player game where some actions are probabilities, some have labels and some have both:
Scope (7)
Basic Uses (4)
Create a three-player game where each choice has a probability:
Create a three-player game where each player only has one action, meaning each of their actions is part of the same information set:
Consider the array of all payoffs:
To determine if a tree game is zero sum, verify that the total payoff is always 0:
Properties (1)
TreeGame objects include properties that give information about the game:
The "Properties" property gives a list of the properties available:
The "Object" property gives the object type of the game:
The "Summary" property gives a brief summary of information about the game:
The "NumberOfPlayers" property gives the number of players in the game:
The "NumberOfActions" property gives the number of actions in the game:
"MinMaxPayoffs" gives the lists of minimum and maximum payoffs for each player:
The "Tree" property gives a Tree representation of the game:
The "Plot" property plots the tree game in the same fashion as the default TreeGamePlot:
The "MatrixGame" property converts any TreeGame into a MatrixGame:
Options (2)
Applications (11)
Historical Games (6)
A prize is concealed behind one of three curtains, and game show host Monty Hall asks you to guess where the prize is. After you guess, Monty opens one of the curtains that does not conceal a prize, leaving closed only your original choice and one other curtain. You are given the option of staying with your original choice or switching to the other closed curtain.
Generate the Monty Hall problem:
The Escalation game is defined as follows. Two nations are in conflict. One nation has the choice to initiate or not initiate, and another nation has the choice to either acquiesce or escalate. Note a third player, "Nature", is often used to portray the randomness of the payoffs. This game is also called the Nuclear game, in reference to the atomic threats during the Cold War.
The Revolution game is defined as follows. A colony has the choice to either rebel of concede to the status quo. The country can either grant independence or suppress the rebellion. If the colony concedes to the status quo, the country can either tax or not tax the colony. This game is usually studied in cases where the payoffs for the suppressed rebellion are unknown.
The Naval Deployment game is an extension of the Battle of Bismarck game to an army that flees and another that is pursuing.
Generate the Naval Deployment game:
Generate a Centipede game with "double-or-nothing" increasing payoffs:
The Beer-Quiche game is a signaling game defined as follows. Player B is considering dueling player A. B does not know whether A is a wimp or surly. B prefers a duel if A is a wimp. Player A wants to avoid a duel. First, B observes whether A chooses to have beer or quiche for breakfast. Both players know that wimps prefer quiche while surly people prefer beer. Note a third player, "Nature", is often used to portray the randomness of the type of A. Moreover, Player A is often called the "sender" of the signal, and player B is the "receiver".
Board Games (2)
Consider a two-by-two game of tic-tac-toe where two adjacent X's or O's are required to win (for example, in
, X wins, but is a tie):Consider the array of all payoffs:
To determine if a tree game is zero sum, verify that the total payoff is always 0:
Consider the tree of all named openings from chess tournaments above 2200 ELO, 2005–2015:
Note the payoffs denote the proportion of games won in these tournaments for each player.
For example, the payoff 
for a given opening implies over all games with that opening, on average, White has won 
of them, Black has won 
of them, and there was a draw in 
of them.
Economics Games (2)
The Entry game is well known in economics and motivates the avoidance of monopolies. A potential entrant chooses whether to enter a market controlled by a monopolist. If the entrant enters, the monopolist can either begin a price war or share the market.
Create the corresponding game:
This is equivalent to the Entry game:
Compute the sub-game perfect equilibrium:
Consider a small firm and a large firm choosing between a high price and a low price for the same product.
Text
Wolfram Research (2025), TreeGame, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeGame.html.
CMS
Wolfram Language. 2025. "TreeGame." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGame.html.
APA
Wolfram Language. (2025). TreeGame. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeGame.html