DSolveで解く微分方程式：はじめに
Wolfram言語関数のDSolveは，微分方程式の記号解を求める．（一方，Wolfram言語関数のNDSolveは，汎用の数値微分方程式ソルバである．）DSolveは以下のような種類の方程式を扱うことができる．
- 常微分方程式(ODE)．独立変数
を1つ，従属変数 
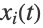を1つ以上持つ．DSolveは常微分方程式系だけでなく，単独の常微分方程式を解くための多岐に渡る手法を備えている． - 偏微分方程式(PDE)．独立変数を2つ以上，従属変数を1つ持つ．偏微分方程式の厳密な記号解を求めることは難しいが，DSolveは標準的な参考文献に見られるほとんどの一階偏微分方程式，およびいくつかの二階偏微分方程式を解くことができる．
- 微分代数方程式(DAE)．系のメンバのうち，微分方程式もあれば，導関数を持たない純粋な代数方程式もある．偏微分方程式の場合と同様に，微分代数方程式の厳密解を求めることは難しいが，DSolveは応用で生じるそのような系の多数の例題を解くことができる．
DSolveは結果を規則のリストとして返す．このため，1つの方程式に複数の解を返すことが可能となる．方程式系では複数の解集合がグループ化されることがある．この規則を使って，解を他の計算に代入することができる．
一般解には，方程式の特殊解を生成するために変化させることのできる任意のパラメータC[i]が含まれる．十分な数の初期条件が指定されると，DSolveは指定された方程式の特殊解を返す．
DSolveの第2引数が，y[x]ではなく y として指定されている場合，解は純関数として返される．この形式は常微分方程式の解を検証したり，後の計算で解を使ったりするのに便利である．詳細は「問題の設定」で説明する．
| DSolve[eqn,u[x,y],{x,y}] |  について偏微分方程式を解く |
常微分方程式の一般解には任意定数が含まれるが，偏微分方程式の一般解には任意関数が含まれる．DSolveではこのような任意関数にC[i]というラベルが付く．
DSolveは微分代数方程式を解くこともできる．シンタックスは，常微分方程式系のものと同じである．
「DSolveで解く微分方程式」チュートリアルの目的
DSolveはモジュール設計である．これは，異なるクラスの問題に対するアルゴリズムが互いに独立に動作するというものである．一旦問題が分類されると（「微分方程式の分類」を参照），そのクラスで使用できるメソッドが決まった順で，解が得られるまで試される．コードは階層構造であり，複雑な問題の解法は，より多数のメソッドが使用できる比較的簡単な問題の解法に簡約される．例えば，高階常微分方程式は，通常その階数を一階か二階に減少させることで解かれる．
記述されるプロセスは内部的に行われ，ユーザの介入は必要としない．このため，このドキュメントの基本的な目的は，以下のようなものである．
- ユーザが最も適した形式でDSolveで問題を解き，その解を研究に適用することができるように，十分な情報やヒントを提供すること．これは，十分な例題を提示することで達成できる．この情報は「DSolveの使用」に要約してある．
- DSolveで扱える問題の種類のリスト，およびそれぞれの場合の解法の特徴を提供する． これは常微分方程式，偏微分方程式，微分代数方程式，境界値問題についてのチュートリアルに記述してある．
「DSolveで解く微分方程式」チュートリアルが，DSolveについての基礎的な知識の習得に役に立ち，より高度なトピックについての情報の参考となれば幸いである．