使用 DSolve 求解微分方程的简介

Wolfram 语言函数 DSolve 求微分方程的符号解. （而另一方面，Wolfram 语言函数 NDSolve 是一个普遍的数值微分方程解算器.）DSolve 可以处理以下类型的方程：

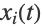  • 常微分方程 （ODEs），即其中只有一个自变量 和一个或者多个应变量 . DSolve 配备了各种不同的技术来求解单个常微分方程以及常微分方程组.
  • 偏微分方程 （PDEs），即其中有两个或多个自变量和一个应变量. 寻找 PDE 的精确符号解是一个难题，但是 DSolve 可以求解大部分的一阶偏微分方程和标准参考书中可以找到的有限数目的二阶偏微分方程.
  • 微分代数方程 （DAEs），其中该方程组的一部分是微分方程，而其余的是纯代数方程，其中并没有导数. 与偏微分方程类似，很难找到微分代数方程的精确解，但是 DSolve 可以求解在应用中出现的这种方程组的许多例子.
DSolve[eqn,y[x],x]对 y[x] 求解微分方程
DSolve[{eqn1,eqn2,…},{y1[x],y2[x],…},x]
对 yi[x] 求解微分方程组

求常微分方程的符号解.

DSolve 返回的结果是一些规则列表. 这样就有可能返回一个方程的多重解. 对于一个方程组，对多重解的集合可能进行分组. 用户可以使用这些规则来将解替换到其它计算中.

这里是求给定的常微分方程的通解. 返回的是满足方程的函数的规则.     
用户可以使用 /. 选出特定的解（ReplaceAll）：

通解包含任意参数 C[i]，改变 C[i] 可以产生方程的特解. 当指定足够数量的初始条件，则 DSolve 返回给定方程的特解.

这里，指定了初始条件 y[0]==1，DSolve 便返回问题的特解：
这里画出解的图形. ReplaceAll (/.) 用在 Plot 命令中，以用方程的解取代 y[x]：
DSolve[eqn,y,x]关于纯函数 y 求解微分方程
DSolve[{eqn1,eqn2,…},{y1,y2,…},x]
关于纯函数 yi 求解微分方程组

求常微分方程作为纯函数的符号解.

当 DSolve 的第二个变量被指定为 y 而不是 y[x] 时，该解作为一个纯函数返回. 这种形式对于验证常微分方程的解、以及在进一步工作中使用该解很有用. 更多详情在 "问题的设置" 中给出.

对于该微分方程的解作为纯函数给出：
这里验证该解：
这里求解常微分方程组. 每个解都根据函数名（这里是 x 和 y）标记，以便更容易选出单个函数：
这里取代自变量的随机值，并且显示在这一点上该解是正确的：
这里画出解的图形：
DSolve[eqn,u[x,y],{x,y}]对于 求解偏微分方程

求偏微分方程的符号解.

常微分方程的通解包含任意常数，而偏微分方程的通解则包含任意函数. DSolve 把这些任意函数标记为 C[i].

这是一个一阶线性偏微分方程的通解. 在该解中，C[1] 标记了 的任意函数：
这里针对 C[1] 的特定选择，获取偏微分方程的特解：
下面是该解的表面图：

DSolve 也可以求解微分代数方程. 其语法与常微分方程组相同.

这里求解一个微分代数方程：
这里对解进行验证：
解的图形显示它们的和满足代数关系 f[x]+g[x]3 Sin[x]：

使用 DSolve 教程求解微分方程的目标

DSolve 的设计是模块化的： 不同类别的问题的算法相互独立. 一旦一个问题已经被分类（如 "微分方程的分类" 中所述），就会用该类中现有的方法按特定的顺序去尝试，直到获取了一个解. 该代码具有分层结构，从而复杂问题的解被降低为相对简单的问题的解，对此可以使用更多不同的方法. 例如，高阶常微分方程通常通过把它们的阶数降低为1或者2来得到求解.

上面所描述的这个过程在内部完成，而不需要用户的任何干预. 为此，这些教程具有下列基本目标.    

  • 提供足够的信息和提示，以便用户可以对 DSolve 提供问题最适当的形式，并且把解用于工作中. 这通过大量实例来实现. 该信息的摘要在 "DSolve 使用介绍" 中给出.    
  • 给出可以被 DSolve 处理的问题的类别以及每个情况下的不同解的性质的目录，这在关于 ODEs、PDEs、DAEs 以及边界值问题（BVPs）的教程中有详细介绍.

这些使用 DSolve 求解微分方程的教程将在获取 DSolve 的基本知识上有所帮助，并且也可以作为在更高级的主题上的信息参考资料.