群論アルゴリズム
このチュートリアルでは,「置換群」で紹介されているアルゴリズム以外の,有限置換群を計算するアルゴリズムを紹介する.
群  の部分群
の部分群 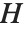 は,
は, の元のリストを
の元のリストを  における
における 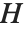 の剰余類と呼ばれる互いに素な部分集合に分割する.これは.
の剰余類と呼ばれる互いに素な部分集合に分割する.これは.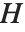 はその部分集合の中の1つであり,残りは
はその部分集合の中の1つであり,残りは  のある任意の元
のある任意の元 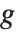 に対して
に対して  (⊙は積の法則)という形式である.剰余類の見分け方には,その剰余類の中で最小の元等,それぞれの剰余類の代表元を選ぶというものがある.
(⊙は積の法則)という形式である.剰余類の見分け方には,その剰余類の中で最小の元等,それぞれの剰余類の代表元を選ぶというものがある.
| RightCosetRepresentative | 剰余類の中で最小の群の元を計算する |
これより大きい群では,すべての置換をリストしたり順位付けしたりすることはできないが,それでもRightCosetRepresentativeは使うことができる.
| GroupCentralizer | ある群の元の中心化群を計算する |
群  の点の固定部分群は,作用領域にある1つ以上の点の集合を固定する
の点の固定部分群は,作用領域にある1つ以上の点の集合を固定する  の元の部分群である.この概念は,それらの点を固定している元,あるいはそれらの点をその中で動かしている元の部分群である,固定群にまで拡張することができる.
の元の部分群である.この概念は,それらの点を固定している元,あるいはそれらの点をその中で動かしている元の部分群である,固定群にまで拡張することができる.
| GroupSetwiseStabilizer | 点のリストの固定部分群を計算する |