群论算法
本教程介绍一些不同于 "置换群" 教程中的计算有限置换群的一些基本算法.
群  的子群
的子群 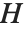 把
把  元素列表分割成不相交的子集,称作
元素列表分割成不相交的子集,称作  中
中 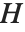 的陪集,
的陪集,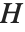 是其中的一个,其余的形式为
是其中的一个,其余的形式为  ,其中
,其中 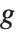 为
为  的某个元素,⊙ 表示乘积律. 识别陪集的一个方法是从每个陪集中选择一个代表,比如陪集中的最小元素.
的某个元素,⊙ 表示乘积律. 识别陪集的一个方法是从每个陪集中选择一个代表,比如陪集中的最小元素.
| RightCosetRepresentative | 计算陪集中的最小群元素 |
对于更大的群,不可能列出或排序所有的置换,但是您仍然可以使用 RightCosetRepresentative.
| GroupCentralizer | 计算某些群元素的中心化子子群 |
| GroupSetwiseStabilizer | 计算点列表的集合式稳定子群 |