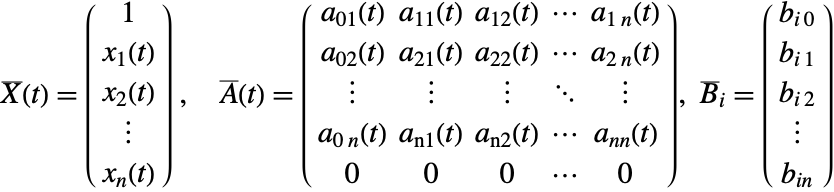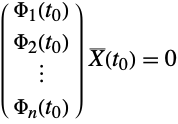境界値問題の数値解法
狙い撃ち法
狙い撃ち("Shooting")法は,境界条件をある点における多変量関数として考え,根を与える初期条件を見付けということに境界値問題を還元することにより作用する.狙い撃ち法の利点は,初期値問題のためのメソッドのスピードと適応性を利用するという点である.しかし,有限差分法や選点法ほどロバストなメソッドではないという欠点もある.成長モードの初期値問題の中には,たとえ境界値問題自体が非常に適切で安定していても,本質的に不安定なものもある.
を考える.狙い撃ち法では ![]() となるような初期条件
となるような初期条件 ![]() が探索される.初期条件を変化させているので,
が探索される.初期条件を変化させているので,![]() は初期条件の関数として考えるのが妥当であり,狙い撃ちは下が成り立つような
は初期条件の関数として考えるのが妥当であり,狙い撃ちは下が成り立つような ![]() を見付けるものと考えることができる.
を見付けるものと考えることができる.
![]() の関数を設定した後で,問題は実際にFindRootに渡され,根を与える初期値
の関数を設定した後で,問題は実際にFindRootに渡され,根を与える初期値 ![]() が探索される.デフォルトメソッドではヤコビアンの計算を含むニュートン法が使われる.ヤコビアンは有限差分を使って計算することができるが,初期値問題の解はその初期条件に敏感で適当に正確な導関数値を得るには影響が大きすぎる可能性があるので,ヤコビアンは常微分方程式の解として計算した方がよい.
が探索される.デフォルトメソッドではヤコビアンの計算を含むニュートン法が使われる.ヤコビアンは有限差分を使って計算することができるが,初期値問題の解はその初期条件に敏感で適当に正確な導関数値を得るには影響が大きすぎる可能性があるので,ヤコビアンは常微分方程式の解として計算した方がよい.
線形化とニュートン法
で記述することができる.ここで ![]() は行列,
は行列,![]() はベクトルでどちらも
はベクトルでどちらも ![]() に依存する可能性がある.
に依存する可能性がある.![]() は定数ベクトル,
は定数ベクトル,![]() は定数行列である.
は定数行列である.
![]() とする.ここで,
とする.ここで,![]() について初期値条件および境界条件両方を微分すると下が得られる.
について初期値条件および境界条件両方を微分すると下が得られる.
![]() は
は ![]() の関数と考えると線形なので,
の関数と考えると線形なので,![]() が得られる.従って
が得られる.従って ![]() となるような
となるような ![]() の値は,どのような特定の初期条件
の値は,どのような特定の初期条件 ![]() の場合についても
の場合についても
非線形問題の場合,![]() を非線形常微分方程式系のヤコビアンとし,
を非線形常微分方程式系のヤコビアンとし,![]() を
を ![]() 番目の境界条件のヤコビアンとする.線形化された系に対する
番目の境界条件のヤコビアンとする.線形化された系に対する ![]() の計算により,特定の初期条件に対する非線形系のヤコビアンが得られ,ニュートン反復へとつながる.
の計算により,特定の初期条件に対する非線形系のヤコビアンが得られ,ニュートン反復へとつながる.
"StartingInitialConditions"
境界値問題では,初期値問題の場合のように一意である保証はない."Shooting"は1つの解だけを見付ける.FindRootが非線形代数方程式系に対して見付ける特定の解に,初期値を変更することで影響が与えられるように,"Shooting"で見付かった解を反復を開始する異なる初期条件を与えることで変更することができる.
"StartingInitialConditions"は"Shooting"メソッドのオプションであり,狙い撃ちプロセスを開始する初期条件の値と位置を指定することができる.
狙い撃ち法はデフォルトでは初期条件なしで開始されるので,解がない場合はそれが返される.
デフォルトで,"Shooting"は区間の左側から始まり,時間を追うごとに前進する.後退した方がよい場合,あるいは区間の中間付近の点から行った方がよい場合もある.
![]() が適切な値の場合,
が適切な値の場合,![]() から始まる初期値問題は
から始まる初期値問題は ![]() および
および ![]() 項が成長するために不安定になる.同様に
項が成長するために不安定になる.同様に ![]() から始めると,前進方向の項ほどは大きくないが,
から始めると,前進方向の項ほどは大きくないが,![]() 項から不安定性が生じる.
項から不安定性が生じる.![]() のある値を超えると,どちらかの方向の感度が大きくなりすぎるために,狙い撃ち法ではよい解が得られなくなる.しかし,その点までなら,両方向での成長がバランスの取れている区間内の点を選ぶことにより,最適な解が得られる.
のある値を超えると,どちらかの方向の感度が大きくなりすぎるために,狙い撃ち法ではよい解が得られなくなる.しかし,その点までなら,両方向での成長がバランスの取れている区間内の点を選ぶことにより,最適な解が得られる.
![]() から"Shooting"を行うと,不正な行列について,さらに境界条件が想定されるように満足されないとの警告が出力される.これは
から"Shooting"を行うと,不正な行列について,さらに境界条件が想定されるように満足されないとの警告が出力される.これは ![]() における小さい誤差が
における小さい誤差が ![]() により増幅されるためである.これの逆数は,局所的切り捨て誤差の大きさの次数と同じなので,このプロットに見られるような可視の誤差は驚くほどのものではない.逆方向では,大きさはずっと小さい
により増幅されるためである.これの逆数は,局所的切り捨て誤差の大きさの次数と同じなので,このプロットに見られるような可視の誤差は驚くほどのものではない.逆方向では,大きさはずっと小さい ![]() であるため,解はずっとよいものである.
であるため,解はずっとよいものである.
選ぶのに適した点は,各方向での感度がバランスの取れている点であり,ここではおおよそ ![]() である.この点では,
である.この点では,![]() の誤差はまだ妥当に制御下におかれる.
の誤差はまだ妥当に制御下におかれる.
オプションの要約
オプション名
|
デフォルト値
| |
| "StartingInitialConditions" | Automatic | 狙い撃ち法を開始する初期座標 |
| "ImplicitSolver" | Automatic | 境界条件により定義された陰的方程式を解くために使われるメソッド.これはFindRootのMethodオプションで取ることのできる値でなければならない |
| "MaxIterations" | Automatic | 陰的ソルバメソッドで使用する反復の回数 |
| "Method" | Automatic | 常微分方程式系の積分に使用するメソッド |
追跡法
追跡("Chasing")法という方法はゲルファント(Gelfand)とロクチェフスキー(Lokutsiyevskii)の原稿に記述されていたもので,初めて英語で[BZ65]に発表され,[Na79]でさらに詳しく説明された.追跡法では,まず1組の補助問題を立て,それを解いて境界のひとつにおける初期条件を求める.一旦初期条件が決まったら,初期値問題を解く通常の方法が適用できる.追跡法は,実質的に,問題の線形性を十分に活用する狙い撃ち法なのである.したがって追跡法は線形微分方程式に使うことができる.
この方程式で,![]() であり,
であり,![]() は係数行列,
は係数行列,![]() は以下のような
は以下のような ![]() 個の線形境界条件を持つ非同次係数ベクトルである.
個の線形境界条件を持つ非同次係数ベクトルである.
ここで ![]() は係数ベクトルである.これから,拡大された同一系を構築する.
は係数ベクトルである.これから,拡大された同一系を構築する.
追跡法とは,![]() と
と![]() が成り立つようなベクトル関数
が成り立つようなベクトル関数![]() を求めることである.一旦関数
を求めることである.一旦関数![]() が分かり,十分な境界条件があれば,以下の式
が分かり,十分な境界条件があれば,以下の式
を解くことで,通常の初期値問題のソルバに用いることができる初期条件![]() を定めることができる.
を定めることができる.![]() の最初の要素が常に1なので,系(3)の解は零ではない点に注意のこと.
の最初の要素が常に1なので,系(3)の解は零ではない点に注意のこと.
このように,境界条件問題を解くことは,![]() についての補助問題を解くことに還元される.
についての補助問題を解くことに還元される.![]() についての式を微分すると,
についての式を微分すると,
これはすべての解 ![]() に当てはまるはずなので,
に当てはまるはずなので,![]() の初期値問題が得られる.
の初期値問題が得られる.
すべての境界値問題の解が求めたいところ を ![]() とすると,Wolfram言語はNDSolveを使うだけで
とすると,Wolfram言語はNDSolveを使うだけで![]() の補助問題を
の補助問題を ![]() まで積分することによって解く.結果は(3)の行列に組み込まれる.これを
まで積分することによって解く.結果は(3)の行列に組み込まれる.これを ![]() について解くと,初期値問題が得られる.この初期値問題をNDSolveで積分すると,返された解が与えられる.
について解くと,初期値問題が得られる.この初期値問題をNDSolveで積分すると,返された解が与えられる.
この方法のこの変形については MathSource パッケージ[R98]でさらに説明が加えられ,使われている.このパッケージを使うと線形固有値問題を解くこともできる.
補助問題を設定するには,これ以外にもGel'fandとLokutsiyevskiiが最初に提唱した方法により近い非線形の方法がある.境界条件が線形に独立であると仮定する(そうでなければ,問題が十分に特定されない).すると,各 ![]() に少なくとも1つの非零の構成要素があることになる.一般性を失うことなく,
に少なくとも1つの非零の構成要素があることになる.一般性を失うことなく,![]() と仮定する.次に,
と仮定する.次に, ![]() の他の構成要素
の他の構成要素![]() の観点から
の観点から![]() について解く.ここで
について解く.ここで![]() であり
であり ![]() である.(5) を使い,
である.(5) を使い,![]() を置き換え,
を置き換え,![]() の他の構成要素の観点から
の他の構成要素の観点から ![]() を考えると,以下の非線形方程式が得られる.
を考えると,以下の非線形方程式が得られる.
上の式で ![]() は
は ![]() から
から![]() 番目の列を除いたものであり,
番目の列を除いたものであり,![]() は
は ![]() の
の![]() 番目の列である.非線形の方法は線形の方法よりも数値的に安定していることがあるが,実数直線上の積分が特異値に至る可能性があるという不都合もある.この問題は複素平面の等高線上で積分することで除外することができるが,複素平面上の積分は実数直線上の単純な積分よりも数値誤差が大きくなることが多いので,実際には非線形の方法の方が線形の方法よりも常によい結果を与えるとはいえない.この理由と,一般的な速さという理由で,Wolfram言語ではデフォルトで線形の方法を使っている.
番目の列である.非線形の方法は線形の方法よりも数値的に安定していることがあるが,実数直線上の積分が特異値に至る可能性があるという不都合もある.この問題は複素平面の等高線上で積分することで除外することができるが,複素平面上の積分は実数直線上の単純な積分よりも数値誤差が大きくなることが多いので,実際には非線形の方法の方が線形の方法よりも常によい結果を与えるとはいえない.この理由と,一般的な速さという理由で,Wolfram言語ではデフォルトで線形の方法を使っている.
通常,境界値方程式がEqualの公差限度を満足することは期待できない.
通常境界条件は,NDSolveのオプションであるAccuracyGoalとPrecisionGoalの最大許容度のときしか満足されない.一般に,確度と精度は大域的ではなく局所的な誤差制御に使われるので,実際の確度と精度はこれよりも劣る.
NDSolveに解のない問題を与えると,数値誤差によってそれが解き得る問題に見えることがある.通常NDSolveは警告メッセージを発する.
方程式が悪条件となる別の例として,境界条件が一意解を与えない場合がある.
通常,Wolfram言語が使うデフォルト値でうまくいくが,NDSolveにオプションMethod->{"Chasing",chasing options}を与えて追跡法をコントロールすることもできる.次は chasing options が取り得る値の表である.
オプション名
|
デフォルト値
| |
| Method | Automatic | 追跡法が生成した初期値問題の計算に使う数値メソッド |
| "ExtraPrecision" | 0 | 補助初期値問題を解くために使う追加精度の桁数 |
| "ChasingType" | "LinearChasing" | 使用する追跡のタイプ."LinearChasing"または"NonlinearChasing" |
NDSolveの"Chasing"メソッドのオプション
メソッド"ChasingType"->"NonlinearChasing"には2つのオプションがある.
オプション名
|
デフォルト値
| |
| "ContourType" | "Ellipse" | 複素平面における積分が必要なときに使用する等高線の形."Ellipse"あるいは"Rectangle" |
| "ContourRatio" | 1/10 | 等高線の長さに対する幅の割合.一般にこの数が小さいほど結果が正確になるが,そうすると方程式を解くのが数値的により困難になる. |
"Chasing"メソッド"NonlinearChasing"オプションのオプション
これらのオプション,特に"ExtraPrecision"は,計算された初期条件に対する感度が強い場合に極めて有効である.
一旦初期条件が見付かると,誤差の大部分は解の計算によるものなので,これ以上精度を上げてもあまり役に立たない.誤差を小さくするためには,NDSolveのAccuracyGoalオプションとPrecisionGoalオプションの値をより厳しくする必要がある.
パラメータを持つ境界値問題
境界値問題が生じるような分野の多くでは,問題自体に,所望の解の一部となり得る固有値等の未定のパラメータがある場合がある.このようなパラメータを従属変数として導入することにより,問題が標準形式の境界値問題として書ける場合がよくある.
例えば,チャネルの流れは次のようにモデル化することができる.
解 ![]() と
と ![]() の値を見付けるためには,方程式
の値を見付けるためには,方程式 ![]() を加えるだけである.
を加えるだけである.