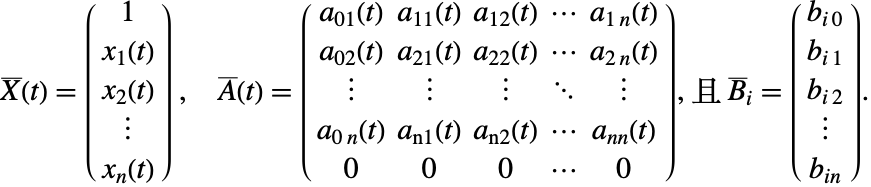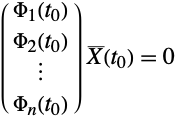“打靶”方法

打靶法的工作原理是：把边界条件考虑为在某些点的初始条件的多变量函数，把边值问题简化为寻找给出一个根的初始条件. 打靶法的优点是它对于初值问题的速度和自适应性优势的利用. 该方法的缺点是它并不像有限差分法或者配置法（collocation method）那么稳健：具有增长模式的一些初值问题本来就不稳定，即使边界问题本身可能是适定的且很稳定.

考虑 BVP 系统

打靶法寻找初始条件 以使得 . 由于用户改变这些初始条件，所以把 考虑为它们的一个函数是有意义的，因此，打靶法可以被视为寻找 使得

在对 建立函数后，问题实际上被传递给 FindRoot 以找到给出根的初始条件 . 默认方法是采用牛顿法，其中涉及雅可比的计算. 虽然雅可比可以采用有限差分计算，一个初值问题（IVP）的解对初始条件太过敏感以致难以获得合理精确的导数值，所以把雅可比作为常微分方程的一个解来计算是有利的.

线性化和牛顿法

线性问题可以描述为：

其中 是一个矩阵，而 是一个向量，它们都可能依赖于 ， 是一个常量向量，而 是常量矩阵.

设 . 然后，对于 IVP 和边界条件关于 的微分给出：

由于 是线性的，当被考虑为 的一个函数，我们有 ，所以使 的 的值对于任意特定初始条件 满足：

对于非线性问题，令 是非线性常微分系统的雅可比，并且令 是第 个边界条件的雅可比. 然后，线性化的系统的 的计算给出一个特定初始条件的非线性系统的雅可比，产生了一个牛顿迭代，

"StartingInitialConditions"

不像初值问题的情况，边值问题没有唯一性的保证. "Shooting" 只能找到一个解. 正如用户可以通过改变初值影响 FindRoot 对一个非线性代数方程找到的特解，用户可以通过给出迭代起始的不同初始条件，改变 "Shooting" 找到的解.

"StartingInitialConditions" 是 "Shooting" 方法的一个选项，它允许用户指定启动打靶过程的初始条件的值和位置.

默认情况下，打靶法从零初始条件开始，这使得如果有一个零解，它将会被返回.

这里计算边值问题 的一个非常简单的解，其中 ：

默认情况下，"Shooting" 从区间的左侧开始，并且朝着时间前进的方向打靶. 在某些情况下朝着后退的方向是有利的，或者甚至在区间中部的某一点也是有利的.

考虑线性边值问题

具有一个解

对于 的适度值，初值问题从 开始变得不稳定，这是因为增长的 和 项. 同样，从 开始，不稳定性从 项出现，虽然它不和前进方向上的项一样大. 在 的一些值之外，打靶不能得到一个好的解，因为在任何一个方向上的敏感度都将太大. 然而，在这些值以内，从区间上选择一个能够平衡两个方向的增长的点将给出最佳解.

这里从默认的 打靶，求解 的系统：

从 打靶，"Shooting" 方法给出关于一个病态矩阵的警告信息，告诉我们边界条件没有如它们应该的那样被满足. 这是因为在 上的一个小误差被放大 倍. 由于它的倒数和局部截断误差具有相同的数量级，如图形中出现的可视误差并不奇怪. 在相反的方向上，放大率将大大减少：，所以解应该会更好.

这里从 打靶计算解：

一个可以选择的很好的点是可以平衡每个方向上敏感度的点，大约在 处. 对此， 时的误差将仍然受到合理的控制.

这里从 打靶计算 的解：

选项总结

"Shooting" 方法选项.    

“追赶” 法

追赶法（The method of chasing）出自于 Gelfand 和 Lokutsiyevskii 首次以英文出版的手稿 [BZ65] 中，并且在 [Na79] 中有进一步的说明. 其思想是建立一个可以被求解以找到一个边界上的初始条件的辅助问题的集合. 一旦确定了初始条件，求解初值问题的常用方法就可以应用. 追赶法实际上是一种最大限度地利用问题具有线性的优势的打靶法. 因此，追赶法可用于求解线性微分方程.

考虑线性常微分方程

其中 ， 是系数矩阵，而 是非齐次系数向量，它具有 个线性边界条件

其中 是一个系数向量. 由此，建立扩充的齐次系统

其中

追赶法归结为寻找一个向量函数 使得 和 . 一旦函数 已知，如果存在边界条件的一个完全的集合，可以用求解

来确定初始条件 ，而该初始条件可以和常用初值问题求解器一起使用. 请注意，系统 (3) 的解是非平凡的，因为 的第一分量总是1.

因此，求解边值问题可以转化为求解关于 的辅助问题. 对 的方程微分给出

代入微分方程，

并且转置

由于这对于所有解 都应该成立，我们得到了 的初值问题，

给定 ，我们想要得到对于所有边值问题在此处的解，Wolfram 语言即使用 NDSolve 通过把 积分到 来求解关于 的辅助问题. 然后，把结果与已经解出 的 (3) 的矩阵相结合来得到初值问题， NDSolve 对该问题积分以得到返回的解.

该方法的这种变种在 MathSource 程序包中有进一步的讨论和使用 [R98]，该变种也允许用户求解线性特征值问题.

有另一个选择，即以一种非线性方式建立接近于 Gelfand 和 Lokutsiyevskii 提出的原问题的辅助问题. 假设边界问题是线性无关的（否则，该问题不能充分确定）. 那么在每个 中，至少有一个非零分量（component）. 不失一般性，假设 . 现在求解用 的其他分量表示的 ，，其中 ， . 使用 (5) 并且替代 ，并采用 的其他分量考虑 ，可以得到以下非线性方程

其中 是删除第 列的 ，而 是A的第 列. 非线性方法可以比线性方法数值上更稳定，但是它也具有缺点，即沿着实线的积分可能会导致奇点. 该问题可以通过沿在复平面中的一个周线（contour）积分来消除. 但是，在复平面上的积分通常具有比沿着实线的简单积分更多的数值误差，所以，在实践中，非线性方法通常不会给出比线性方法更好的结果. 由于这个原因，也因为它一般较快，Wolfram 语言 默认下采用线性方法.

求解器可以求解线性方程组的多点边值问题. （请注意，每个边界方程必须在 的一个特定值上.）

一般说来，用户不能指望边值方程在 Equal 的严格容差内被满足.

它们通常只在来自 NDSolve 的 AccuracyGoal 和 PrecisionGoal 选项的最大容差内被满足. 通常情况下，实际准确度和精确度较低，因为它们是用于局部，而非全局的误差控制.

当用户给 NDSolve 一个无解的问题，数值误差可能使之看起来似乎是一个可解的问题. 通常，NDSolve 会发出一个警告消息.

在这种情况下，它不能在整个区间内积分，因为积分不存在.

另一种方程可能是病态的情况是，当边界条件没有给出一个唯一的解时.

通常情况下，Mathematica 所采用的默认值表现良好，但是用户可以通过给出 NDSolve 的选项 Method->{"Chasing",chasing options} 来控制追赶法. 可能的 chasing options 如下表所示.

NDSolve 的 "Chasing" 方法的各种选项.

方法 "ChasingType"->"NonlinearChasing" 本身具有两个选项.

"Chasing" 方法的 "NonlinearChasing" 选项的各种选项.

这些选项，特别是 "ExtraPrecision"，在对算得的初始条件有很强的敏感性的情况下，会很有用.

在此之外增加额外的精确度不会真的有用，因为误差中的很大一部分来自于一旦找到初始条件后对解的计算. 若要减少误差，用户需要对 NDSolve 给出更严格的 AccuracyGoal 和 PrecisionGoal 选项.

具有参数的边值问题

在出现边值问题的许多应用中，问题本身可能有不确定的参数，比如特征值，而些参数可能是理想的解的一部分. 通过引入作为应变量的参数，问题往往可以写成标准形式的边值问题.

例如，在一个通道中的流体可以通过下式建模

其中 （雷诺数）已给出，但是 尚待确定.

若要求解 和 的值，只需添加方程 .

这里对 的流体问题求解 和 ，画出 的解，并返回 的值：