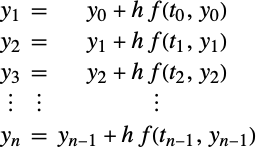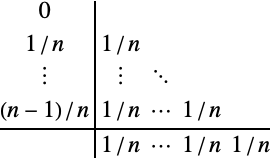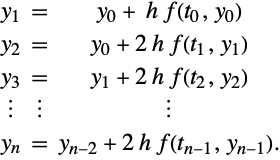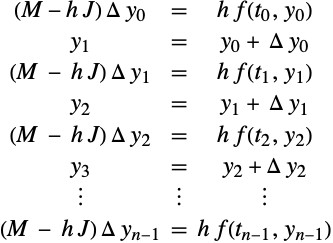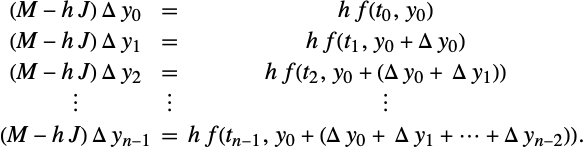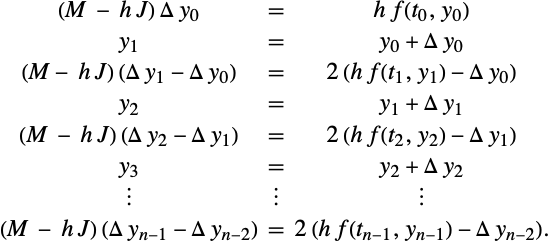NDSolveの"Extrapolation"メソッド
はじめに
外挿法とは，次数と刻み幅が自動制御される任意次数のメソッドのひとつである．誤差推定は，同じメソッドをさまざまなステップ数で使い，計算された解全体にフィットする多項式の外挿を使って，任意区間上の解を計算することで生じ，複合的な高次法を与える[BS64]．また，この多項式は誤差推定の方法を提供する．
一般に低精度では，外挿法はルンゲ・クッタ型のメソッドに及ぶものではなかった．しかし，高精度で任意次数法を使うということは，非常に正確な許容誤差の計算では固定次数法を使うよりも格段に速くなり得るということである．
次数および刻み幅の制御は，[HNW93]と[HW96]に記述されているコードodex.fとseulex.fに基づいている．
"Extrapolation"
"DoubleStep"法は各1ステップの積分法にリチャードソン(Richardson)の補外を1度実行する．これは「NDSolveのDoubleStep法」内に記述されている．
"Extrapolation"は，リチャードソンの補外を一連の微調整に一般化するものである．
を基本的な刻み幅とし，次のように正の整数の単調増加列を選ぶ．
で定義する．次に次数 
の数値法を選び，刻み幅 
で 
ステップ実行することにより初期値問題の解を計算すると，以下が得られる．
値の表を構築することにより，Aitken–Nevilleアルゴリズムを使って外挿が実行される．
ここで 
は，基本メソッドが補外のもとで対称かどうかにより1か2のいずれかになる．
硬くない問題では，(2)の 
の次数は 
である．硬い問題では，分析はもっと複雑であり，特異な振動問題に現れる振動項の調査が必要になる[HNW93, HW96]．
外挿の数列
外挿の数列は，実装で指定することができる．以下は，一般的に使われる数列の例である．
を満足する数列には，
次の基本積分法の丸め誤差を最小化する効果がある．
最低コストの数列は調和数列である．しかし丸め誤差が捨てられないので，問題がないわけではない．
丸め誤差の累積
高次の外挿では，Aitken–Nevilleアルゴリズム(3)における丸め誤差の累積を考慮することが大切である．
[HNW93]のセクションII.9のExercise 5を例に取る．
項目 
が丸め誤差 
を持ち，これらの誤差の外挿表の中への伝播を計算するとする．
外挿過程(4)は線形なので，
はゼロに等しく，
を取ると仮定する．
以下は，調和数列と対称二次基本積分法 
を使用して，初期データ上のAitken–Nevilleアルゴリズム(5)の進化を示している．
16次のメソッドでは，丸め誤差の累積のためにおよそ2桁が失われてしまう．
このモデルは幾分大雑把なものである．というのも，「丸め誤差の軽減」で説明するように，丸め誤差は 
のとき 
ではなく 
で生じることの方が多いからである．
丸め誤差の軽減
ここで，高次の外挿における丸め誤差による効果が軽減できるアプローチを探すのも意味のあることである．
ひとつのアプローチとして，丸め誤差を小さくするために異なるステップシーケンスを選ぶというものがある．しかしこれには，外挿表の最初の列に 
を形成するのに必要な積分ステップ数が多くなるという欠点がある．
STEP等，コードの中には，厳しい許容誤差に対する丸め誤差の効果を軽減するために積極的な方法を取るものもある [SG75]．
別の方法として，外挿ということにおいてはそれほどの注目を集めてはいないが，浮動小数点操作における丸め誤差の大きさを減少させるために，基本積分法を修正するというものがある．このアプローチは[G51]の考えに基づいており，2体問題[F96b]で使われている．（背景は[K65]，[M65a]，[M65b]，[V79]も参照のこと）次のセクションでは，これについて説明する．
基本メソッド
以下のメソッドは，外挿の基本積分法として一般的に選ばれるものである．
効率性を考えて，これらのメソッドはNDSolveに組み込まれており，Methodオプションで別々のメソッドとして呼び出すことができる．
上記のメソッドの実装には，"DoubleStep"および"Extrapolation"内の複数のサブステップに対する特殊な解釈が含まれる．
1ステップメソッドに対するNDSolveフレームワークでは，増分あるいは解のアップデートを返す公式が使われる．これは，数値誤差が長期に渡る積分で取り除かれない幾何的数値積分に有利である．またこれは，補償される総和等の効率的補修ストラテジーの適用を許可する．この式も補外のコンテキストで便利である．
多段階のオイラー(Euler)法
，
，
があるとき，刻み幅 
の 
回の連続した積分ステップがオイラー法で実行されるとする．
陽的ルンゲ・クッタ法との一致
ある基本積分スキームでは，(9)から生成された外挿表の項目 
は，陽的ルンゲ・クッタ法と一致するということがよく知られている（[HNW93]のセクションII.9のExercise 1を参照）．
再定式化
とすると，積分(11)は陽的ルンゲ・クッタ法(12, 13)との一致を反映するために以下のように書き換えることができる．
ここで(14)の右辺の項は，同値の 
から逸脱するものと考えられる．
数学的に言うと，公式(17)と(18, 19)は等しい．しかし 
のとき，(20)の計算の方が有限精度の浮動小数点演算の丸め誤差累積を軽減させる 
の数量（増分）の累積和が小さいという利点がある．
多段階法の陽的中点公式
リチャードソンの補外を効果的に実装するためには，
の偶数乗での拡大が非常に重要である[S70]．
一段階のオイラー法の後に多段階法の陽的中点公式を使って実行される刻み幅 
の連続した積分ステップ 
を考える．
(21)を
段階の中点公式で計算すると，メソッドには誤差の対称拡大が含まれる([G65], [S70])．
再定式化
グラッグ法（平滑法）
グラッグ法は，陽的中点公式が安定ではないということに歴史的起源がある．
(23)を利用するためには，公式(24)を
段階の中点公式で計算する．これには安定領域を増大し，基本ステップの最後で関数を評価するという利点がある[HNW93]．
構造上の理由で，増分の和と2つの連続した増分がアルゴリズムの最後で利用可能になる点に注目のこと．これにより，以下の公式が導かれる．
さらに(25)は，有限精度の計算では(26)よりも有利である．それは，通常増分
よりも大きい値 
が計算に関与しないためである．
グラッグ法は，メソッドの後に外挿を使う場合はそれほど重要ではない．これよりもShampineの提案する平滑法の方がわずかに効率的である[SB83]．
"ExplicitMidpoint"メソッドは
段階法を使い，"ExplicitModifiedMidpoint"メソッドは
段階法使った後で平滑法(27)を使う．
安定領域
以下は，平滑法が線形安定領域に及ぼす影響を示したものである（FunctionApproximations.mパッケージを使って実行）．
任意の基本メソッドに対する正確な安定境界は計算が複雑なので，簡単な近似が用いられる．次数 
の補間メソッドでは，負の実軸の交点がその点と考えられる．ここでは以下が成り立つ：
安定領域は負の半平面の場合，この半径で原点が(0,0)の円板として近似される．
陰的微分方程式
微分方程式系の一般化(28)は放物型偏微分方程式の空間離散化等多くの状況で発生する．
線形方程式系の解を含む補外の基本メソッドは，形式(29)の問題を解くよう簡単に変更することができる．
線形多段階の後退オイラー法
多くの半陰的および陰的手法の記述では，増分は自然に発生する．
および 
である系(30)に対する線形後退オイラー法を使って実行される連続した積分ステップを考えてみる．
(31)の増分に対する方程式の解は，行列 
のLU分解を1度，それに続き各右辺の三角線形系の解を使うことにより得られる．
再定式化
からの出発した増分の再定式化は，以下のように求めることができる．
で 
のとき，(35)と(36)は等価であることに注目のこと．
線形多段階の陰的中点公式
BaderとDeuflhardの公式[BD83]を使って，線形陰的オイラー法に続く 
および 
である線形多段階の陰的中点公式の1ステップを考える
線形
段階の陰的中点法で(37)を計算すると，メソッドには誤差の対称拡大が含まれる[BD83]．
再定式化
増分に関する(38)の再定式化は，以下のように求めることができる．
平滑法
線形の陰的中点公式に適した平滑法は[BD83]である．
増分に関して書き直されたBaderの平滑法(39)は，以下のようになる．
線形の陰的中点公式の平滑法は，陽的中点公式のグラッグの平滑法とは異なる役割を持つ（[BD83]と[SB83])を参照）．前者には排除の必要がある安定ではない項がないので，その目的は漸近安定性を向上させることである．
"LinearlyImplicitMidpoint"メソッドは
段階法を使い，"LinearlyImplicitModifiedMidpoint"メソッドは
段階法の後で平滑法(41)を使う．
増分による多項式の外挿
増分によって外挿表の第1列の項目である 
を修正する方法は，前述の通りである．
しかし，ある基本的積分法では，
のそれぞれが陽的ルンゲ・クッタ法に対応する．
従って，その関係がまだ完全に利用されておらず，さらなる微調整が可能なようである．
Aitken–Nevilleアルゴリズム(42)には線形差分方程式が含まれるので，増分を使って外挿プロセス全体が実行できる．
これにより，以下のようなAitken-Nevilleアルゴリズムの修正が導かれる．
(43)の数量
は，修正された基本積分法から得られた初期量 
から始めて，
の影響を受けることなく繰り返し計算できる．
この利点は，外挿表が小さい数量で構築されているため，減算の桁落ちによる丸め誤差の効果が，減少する．
実装の問題
実装の問題として考慮すべきものが多くあるが，そのいくつかをここに挙げる．
ヤコビアンの再利用
ヤコビアンは，それ自身とそれが評価される関連時間とを共に保存することにより，各時間刻みにおけるすべての項目 
について1度だけ評価される．これには，拒絶されたステップについてはヤコビアンを再計算する必要がないという利点がある．
密な線形代数
密な系では，LU分解にはLAPACKルーチンのxyyTRFが，その結果の三角方程式系にはxyyTRSが使える[LAPACK99]．
次数の適応法と作業推定
積分の過程で外挿の次数を適宜変更するためには，基本スキームと外挿の列に必要な作業量を測定することが大切である．
線形の陰的スキームで各線形系を解くコストを考慮に入れるためには，系の次元（できれば構造に従った重み付きで）を組み入れる必要がある．
安定性のテスト
外挿法は，問題を引き起す可能性のある大きな基本刻み幅を使う．
「どちらのコードもオーバーフローを起すので，ファン・デル・ポル(Van der Pol)方程式を解くことはできない」[S87]．
線形の陰的基本スキームには2つの形式の安定性テストが使われる（追加説明は[HW96]を参照のこと）．
Deuflhardは，
の計算を中断するためには，完全に陰的なスキームに適用されたニュートン反復が収束するかどうかを判定すればよいと提案している．
(44) は(45)と2つ目の方程式だけが異なる．異なる右辺の解を見付けなければならないが，関数評価を追加する必要はない．
陰的中点公式
，
では，単に基本演算操作を数回必要とするだけである．
どちらの安定性テストの形式の実装でも，増分公式の方が正確である．
例題
作業誤差比較
増分公式
この例には，調和数列を持つ八次の"ExplicitEuler"が含まれている．外挿の過程で増分ベースの公式を使うことにより，精度がおよそ2桁向上している．
外挿の過程で増分ベースの公式を使うことにより，精度がおよそ2桁向上している．
以下は前出の例題の外挿表の最初の列を形成する積分データの相対誤差を比較したものである．
参照値は32桁のソフトウェア演算を使って計算され，最近傍のIEEE倍精度浮動小数点数に変換された．ここでULPとはUnit in the Last PlaceあるいはUnit in the Last Position（最後の桁の単位）を意味する．
実際には，
の誤差が1ULPを超える可能性があるので，丸め誤差の増大の研究の動機として使われた丸め誤差モデルには限界があるという点に注目する．
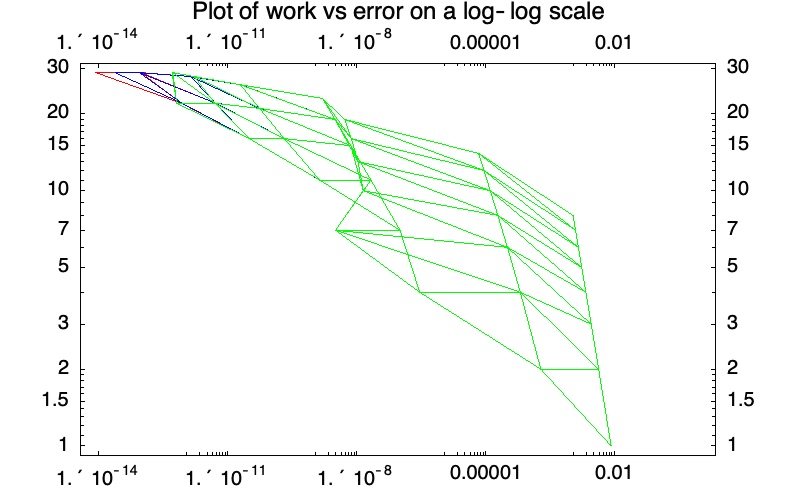
メソッドの比較
ここでは"ExplicitEuler"（赤），"ExplicitMidpoint"（青），"ExplicitModifiedMidpoint"（緑）のそれぞれに基づく外挿に必要な作業を比較する．
次数の選択
メソッドの比較
硬い系
ヤコビ行列が自動的に計算され（数値差分あるいは記号微分を使ってユーザが指定できる），ランタイム時に適切な線形代数ルーチンが選ばれ実行される．
高精度の比較
質量行列 - fem2ex
整数 
が 
を定義し，Galerkinの離散化法を使って 
の 
において近似する：
(51)に適用された離散化(52)は(53)のような定数質量行列式を持つ常微分方程式系になる．常微分方程式系は[SR97]におけるfem2ex問題であり，IMSLライブラリでも見られる．
上で解かれる：微調整
"StepSizeSafetyFactors"
ほとんどのメソッドでそうであるように，あまりに小さいステップと，通常は拒否されるほどの大きいステップとの間でバランスを取りたいと思うであろう．"StepSizeSafetyFactors"->{s1,s2}オプションは以下のようにして，刻み幅の選択を制約する．次数 
のメソッドによって選ばれた刻み幅は，以下を満足する．
"StepSizeRatioBounds"
オプション"StepSizeRatioBounds"->{srmin,srmax}は以下のように，次の刻み幅の範囲を指定する．
"OrderSafetyFactors"
"Extrapolation"の重要な一面に，次数の選択というものがある．
陽的な基本メソッドの作業推定は，関数評価の回数と使われるステップシーケンスに基づいている．
線形陰的な基本メソッドの作業推定は，ヤコビアンの評価のコスト，LU分解のコスト，線形方程式の逆計算のコストも含んでいる．
単位ステップあたりの作業推定は，作業推定 
と次数 
のメソッドで取る新しく使う推定刻み幅 
（(54)から計算される）から形成される．
は連続した推定値を比較して，別の次数のメソッドの方が効率的となる時期を決定する．
オプション"OrderSafetyFactors"->{f1,f2}は，推定値 
の比較に含まれる安全率を指定する．
この他にも，いつステップあたりの次数の最大増加が1（対称法では2）となるか，ステップが拒絶された直後に，いつ次数の増加を禁止するか等の制約がある．
ノンスティッフな基本メソッドでは，デフォルト値は{4/5, 9/10}であり，スティッフな基本メソッドでは{7/10, 9/10}である．
オプションの要約
オプション名
|
デフォルト値
| |
| "ExtrapolationSequence" | Automatic | 外挿で使う数列を指定する |
| "MaxDifferenceOrder" | Automatic | 使用する最大次数を指定する |
| Method | "ExplicitModifiedMidpoint" | 使用する基本積分法を指定する |
| "MinDifferenceOrder" | Automatic | 使用する最小次数を指定する |
| "OrderSafetyFactors" | Automatic | 適応型の次数選択の推定で使う安全率を指定する |
| "StartingDifferenceOrder" | Automatic | 使用する初期次数を指定する |
| "StepSizeRatioBounds" | Automatic | 下限 上限のときに，現在の刻み幅  から新しい刻み幅  への相対変化の境界を指定する |
| "StepSizeSafetyFactors" | Automatic | 適応型刻み幅に使う誤差推定に組み込む安全率を指定する |
| "StiffnessTest" | Automatic | 硬さ検出機能を使うかどうかを指定する |
"ExtrapolationSequence"オプションのデフォルト設定Automaticでは，基本メソッドの硬さと対称性に基づいて列が選ばれる．
"MaxDifferenceOrder"オプションのデフォルト設定Automaticは，最大次数を十進の作業精度の2倍に制限する．
"MinDifferenceOrder"オプションのデフォルト設定Automaticは，基本メソッドの次数から始めた2つの外挿の最小を選ぶ．
"OrderSafetyFactors"オプションのデフォルト設定Automaticは，硬い基本メソッドには値{7/10,9/10}を，硬くない基本メソッドには値{4/5,9/10}を使う．
"StartingDifferenceOrder"オプションのデフォルト値Automaticは，"MinDifferenceOrder" 
の設定により異なる．これは，基本メソッドが対称であるかどうかにより，
か 
に設定される．
"StepSizeRatioBounds"オプションのデフォルト設定Automaticでは，硬い基本メソッドには値{1/10,4}が，硬くない基本メソッドには値{1/50,4}が使われる．
"StepSizeSafetyFactors"オプションのデフォルト設定Automaticは，硬い基本メソッドには値{9/10,4/5}を，硬くない基本メソッドには値{9/10,13/20}を使う．
"StiffnessTest"オプションの基本設定Automaticは，硬くない基本メソッドが使われるならば硬さ検定が有効になることを意味する．
オプション名
|
デフォルト値
| |
| "StabilityTest" | True | 連続した陰的な解（例(55)を参照）に安定性テストを実行するかどうかを指定する |
"LinearlyImplicitEuler"，"LinearlyImplicitMidpoint"，"LinearlyImplicitModifiedMidpoint"の各メソッドのオプション