"DoubleStep" Method for NDSolve
Introduction
The method "DoubleStep" performs a single application of Richardson's extrapolation for any one-step integration method.
Although it is not always optimal, it is a general scheme for equipping a method with an error estimate (hence adaptivity in the step size) and extrapolating to increase the order of local accuracy.
"DoubleStep" is a special case of extrapolation but has been implemented as a separate method for efficiency.
- The correction term
 can be used for error estimation enabling an adaptive step-size scheme for any base method.
can be used for error estimation enabling an adaptive step-size scheme for any base method.
- If the base numerical integration method is symmetric, then the improved approximation has order
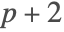 ; otherwise it has order
; otherwise it has order 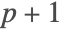 .
.
Examples
Extending Built-in Methods
The method "ExplicitEuler" carries out one integration step using Euler's method. It has no local error control and hence uses fixed step sizes.
User-Defined Methods and Method Properties
Integration methods can be added to the NDSolve framework.
In order for these to work like built-in methods it can be necessary to specify various method properties. These properties can then be used by other methods to build up compound integrators.
Method properties used by "DoubleStep" are now described.
Order and Symmetry
Without knowing the order of the base method, "DoubleStep" is unable to carry out Richardson's extrapolation.
The order of the result of Richardson's extrapolation depends on whether the extrapolated method has a local error expansion in powers of ![]() or
or ![]() (the latter occurs if the base method is symmetric).
(the latter occurs if the base method is symmetric).
If no method property for symmetry is defined, the "DoubleStep" method assumes by default that the base integrator is not symmetric.
Stiffness Detection
Details of the scheme used for stiffness detection can be found within "StiffnessTest Method Option for NDSolve".
Stiffness detection relies on knowledge of the linear stability boundary of the method, which has not been defined.
Computing the exact linear stability boundary of a method under extrapolation can be quite complicated. Therefore a default value is selected which works for all methods. This corresponds to considering the p th order power series approximation to the exponential at 0 and ignoring higher order terms.
- If "LocalExtrapolation" is True then a generic value is selected corresponding to a method of order p + 2 (symmetric) or p + 1.
- If "LocalExtrapolation" is False then the property "LinearStabilityBoundary" of the base method is checked. If no value has been specified then a default for a method of order p is selected.
Higher Order
The following example extrapolates the classical Runge–Kutta method of order four using two applications of (3).
The inner specification of "DoubleStep" constructs a method of order five.
A second application of "DoubleStep" is used to obtain a method of order six, which uses adaptive step sizes.
In general the method "Extrapolation" is more appropriate for constructing high-order integration schemes from low-order methods.
Option Summary
option name | default value | |
| "LocalExtrapolation" | True | specify whether to advance the solution using local extrapolation according to (4) |
| Method | None | specify the method to use as the base integration scheme |
| "StepSizeRatioBounds" | { | specify the bounds on a relative change in the new step size hn+1 from the current step size hn as low ≤ hn+1/hn ≤ high |
| "StepSizeSafetyFactors" | Automatic | specify the safety factors to incorporate into the error estimate (5) used for adaptive step sizes |
| "StiffnessTest" | Automatic | specify whether to use the stiffness detection capability |
Options of the method "DoubleStep".
The default setting of Automatic for the option "StiffnessTest" indicates that the stiffness test is activated if a nonstiff base method is used.
The default setting of Automatic for the option "StepSizeSafetyFactors" uses the values {9/10,4/5} for a stiff base method and {9/10,13/20} for a nonstiff base method.