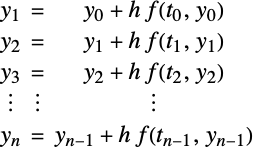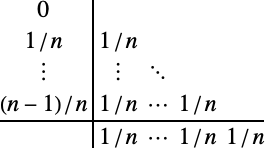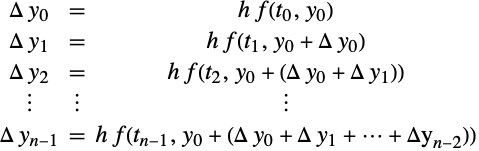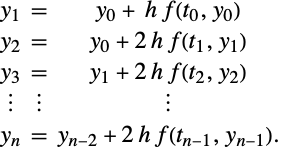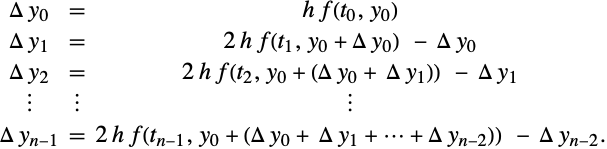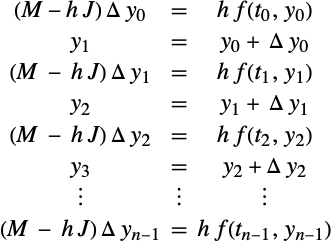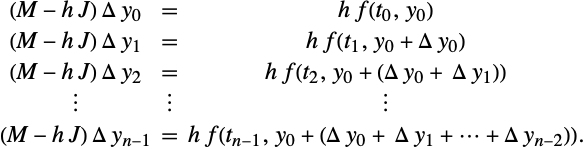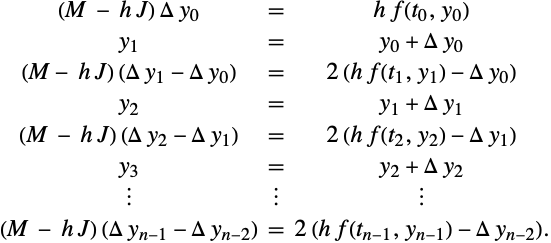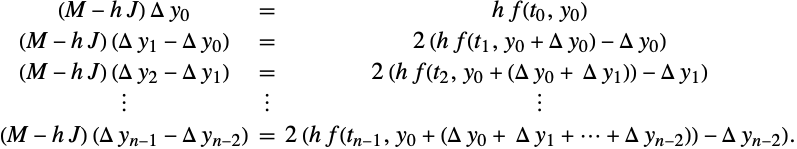引言

外插法是一类任意阶数的方法，它具有自动的阶数和步长控制. 误差估计来自使用具有一个变化的步进数目的同样的方法以及使用在计算所得解上拟合的多项式的外插法的在一个区间上对解的计算，产生了一个复合高阶方法 [BS64]. 同时，多项式给出了误差估计的一种方法.

通常，对于低精度，外插法还没有到可以与朗格-库塔类型方法竞争的程度. 但是，对于高精度，任意阶数意味着对于非常精确的容差，它们可以比固定阶数的方法相应地更快.

阶数和步长控制基于 [HNW93] 和 [HW96] 中描述的代码 odex.f 和 seulex.f.

"Extrapolation"

方法 "DoubleStep" 对任意一步积分方法执行单个 Richardson 外插法的应用，并且在 "NDSolve 的 “DoubleStep”方法" 中详细介绍.

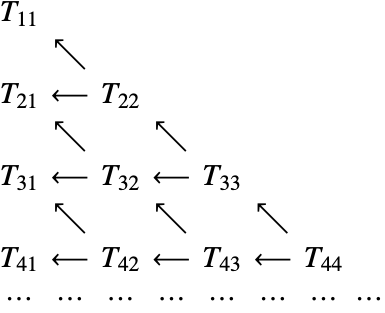
"Extrapolation" 把 Richardson 外插法的思想推广到一系列细化中.

考虑一个微分系统

令 为一个基本步长；选择一个由正整数组成的单调递增序列

并且定义相应的步长

满足

选择一个阶数为 的数值方法，并且通过执行 步、步长为 的操作计算初值问题的解，以得到：

外推法是通过建立一个值为：

的表，使用 Aitken–Neville 算法执行. 这里 是 1 或者 2 ，取决于基本方法在外插法下是否是对称的.

(1) 中的值的一个依赖图说明了其关系.

考虑 、、 等价于 Richardson 外推法.

对于非刚性问题，(2) 中 的阶数是 . 对于刚性问题，分析就更加复杂，它涉及了在奇异摄动问题中出现的扰动项的探究 [HNW93, HW96].

外推序列

任何外推序列都可以在实现中指定. 一些常见的选择如下.

满足 的一个序列具有对阶数 基本积分方法的舍入误差最小化的效果.

具有最低成本的序列是调和序列，但这并非没有问题，因为舍入误差没有衰减.

舍入误差累积

对于高阶外插法，一个重要的考虑是Aitken-Neville算法（2）中的舍入误差的积累.

作为一个例子，考虑 [HNW93] 中的第II.9节的练习5.

假设项 受到舍入误差 的扰动，并且把这些误差的传播计算到外插表格中.

由于外插过程（3）的线性性，假定 等于0，并且令 .

这里显示了Aitken-Neville算法（2）使用调和序列和一个对称二阶基本积分方法， 在初始数据上的演化.

因此，对于一个16阶方法，由于舍入误差累积，将近两个小数数字丢掉了.

这种模型有些粗糙，因为正如用户将在 "舍入误差的减少" 中看到的，对于 ，舍入误差更有可能在 而不是 中生成.

舍入误差的减少

看来寻找可以用来减少高阶外插法中的舍入误差的方法是值得的.

选择一个不同的步进序列来减少舍入误差是一种方法，虽然其缺点是在外插表格的第一列形成 所需的积分步骤的数目要求更多的工作.

一些代码，例如 STEP，采取主动的策略来减少严格容差中的舍入误差的影响 [SG75].

另一种在外插法的讨论中并没有受到太大关注的策略，就是要修改基本积分方法，以减少在浮点运算中的舍入误差的大小. 这种基于可追溯到 [G51]的思想，并且用来达到 [F96b]中两体问题的良好效果的方法，在接下来进行解释（有关取背景，请参阅 [K65], [M65a], [M65b], [V79]）.

基本方法

下面方法是外插法中基本积分器最常见的选择.

• "ExplicitEuler"

• "ExplicitMidpoint"

• "ExplicitModifiedMidpoint" （Gragg 平滑化步骤（40））

• "LinearlyImplicitEuler"

• "LinearlyImplicitMidpoint" （不具有平滑化步骤的Bader–Deuflhard 表述（17））

• "LinearlyImplicitModifiedMidpoint" （具有平滑化步骤的 Bader–Deuflhard表述（17））

为了提供效率，这些方法已经被构建到 NDSolve 中，并且可以通过 Method 选项作为单个方法调用.

这些方法的实现对于 "DoubleStep" 和 "Extrapolation" 中的多个子步具有一个特殊的解释.

一步方法的 NDSolve 框架使用一个返回解的增值或者更新的表述. 这对于数值误差没有在长时间积分上衰减的几何数值积分是有利的. 这也允许有效地应用诸如补偿总和的修正策略. 这种表述对于外插法的情况也是有用的.

这些方法与用来减少舍入误差累积的增量重组一同描述.

多个欧拉步骤

给定 、 和 ，考虑 的一系列积分步，其步长为 ，该积分步使用欧拉方法实现：

其中 .

与显式朗格-库塔方法的关联

众所周知，对于某些基本积分方案，从（2）中产生的外插表格中的项 对应于显式朗格-库塔方法（参阅 [HNW93] 中的第II.9节，练习1）.

例如，(5) 等价于一个 -阶段显式朗格-库塔方法：

其中，系数使用 Butcher 表格表示：

重组

令 . 那么积分 (6) 可以重新改写成：

以反映与一个显式朗格-库塔方法 (7, 8) 的关联. 其中，(9) 的右侧的项现在被认为是从同样的 值的偏差（departure）.

（10）中的 对应于（1）中的 .

令 ；那么要求的结果可以复原为：

数学上，公式（11）和（12, 13）是等价的. 然而，对于 ，（14）中的计算具有累积较小的 量和或者增量和的优势，这降低了有限精度浮点算术的舍入误差的累积.

多个显式中点步骤

的偶数幂展开对于理查森外插法的有效实现是非常重要的，[S70] 中给出了一个巧妙的证明.

考虑一系列积分步 ，其步长为 ，该积分步使用一个欧拉步后跟随多个显式中点步来执行：

如果（15）使用 个中点步计算，那么该方法具有一个对称的误差展开 ([G65], [S70]).

重组

（16）的重组可以以增量的形式实现，如下所示：

Gragg 平滑化步骤

Gragg 的平滑化步骤（smoothing steps）的历史渊源在于显式中点规则：

的弱稳定性. 为了使用（1），公式（1）使用 个步骤计算. 这具有增加稳定性区域以及在基本步骤的末尾计算函数的优势 [HNW93].

注意，由于构建的原因，在该算法末尾，伴随着两个连续的增量有一个增量的和可资利用. 这导致下列公式：

此外，（17）比（1）具有在有限精度运算方面的优势，因为通常比增量 更大的 值，对计算没有贡献.

Gragg 平滑化步骤，如果后面跟着外插法的话，并不是很重要. Shampine 提出了另外一种稍微有效一些的平滑程序 [SB83].

方法 "ExplicitMidpoint" 采用 个步骤，而 "ExplicitModifiedMidpoint" 使用 个步骤，随后是平滑化步骤（18）.

稳定性区域

下图显示在线性稳定性区域中的平滑化步骤的效果（使用程序包 FunctionApproximations.m 实现）.

显式中点规则（左侧）和带有平滑化的显式中点规则（右侧）对 的线性稳定性区域：

由于精确的稳定性边界的计算对于一个任意基本方法可能很复杂，我们使用一个更简单的近似. 对于一个阶数为 的外插法，与负实轴交点可以认为是满足下式的点：

稳定性区域近似为一个对于负半平面，以次为半径以，原点为（0，0）的圆盘.

隐式微分方程

微分系统（1）的推广出现在许多情况中，比如抛物型偏微分方程的空间离散化：

其中 是一个常量矩阵，常常被称为质量矩阵（mass matrix）.

涉及线性方程组的求解的外插法中的基本方法可以很容易地被修改以求解具有形式（1）的问题.

多个线性隐式欧拉步骤

增量在许多半隐式和隐式方法的描述中自然地出现. 考虑对 和 的系统（1）使用线性隐式欧拉方法执行的一系列积分步骤.

这里 表示质量矩阵，而 表示 的雅可比矩阵：

（19）中增量的方程的求解是通过使用矩阵 的一个LU分解，后对各式右边的三角形线性系统求解来实现的.

从（20）得到的预期的结果为：

重组

用作为从 偏离的增量的形式的重组可以通过如下方式实现：

使用（1）的 的结果是从（2）得到的.

注意，当 、 时，（1）和（1）是等价的.

多个线性隐式中点步骤

考虑一个步骤的线性隐式欧拉方法，后跟随多个线性隐式中点步骤，其中 和 ，并使用 Bader 和 Deuflhard 的公式 [BD83]:

如果对于 (21) 通过 个线性隐式中点步进行计算，那么该方法具有一个对称的误差展开 [BD83].

重组

用增量的形式对(22) 的重组可以通过如下方式实现：

平滑化步骤

对于线性隐式中点规则的一个适当的平滑化步骤是 [BD83]

用增量的形式重写的 Bader 平滑化步骤（1）成为：

当（1）使用 个步骤运行时，得到要求的量.

用于线性隐式中点规则的平滑化步骤具有一个与用于显式中点规则的Gragg平滑化不同的角色（参阅 [BD83] 和 [SB83]）. 由于没有弱稳定项来消除，其目的是提高渐近稳定性.

方法 "LinearlyImplicitMidpoint" 使用 个步，而 "LinearlyImplicitModifiedMidpoint" 使用 个步，其后跟随平滑化步骤（2）.

使用增量形式的多项式外插法

用户已经看到如何在外插表格的第一列中用增量的形式修改 .

但是，对于某些基本积分方法，每个 对应于一个显式朗格-库塔方法.

因此，可以看出关联还没有完全开发，进一步的完善是可能的.

由于 Aitken–Neville算法（23）包含线性差分，整个外插过程可以用增量执行.

这导致 Aitken–Neville算法的下列修订：

（1）中的量 可以从由修正的基本积分方案不加 的贡献得到的初始量 开始迭代计算.

最终期望值 可以以 的形式得到.

这里的优点是外插表格使用较小的量建立，因此源于相减抵消的舍入误差效果被减弱.

实现问题

有许多重要的实现问题应该考虑，其中一些在这里提到.

雅可比重用

雅可比只在每个时间步骤通过把它与计算相关的时间一起存储，对所有项 计算一次. 这也有优点，即雅可比不需要对被拒步重新计算.

稠密线性代数

对于稠密系统，LAPACK 例程 xyyTRF 可以用于 LU 分解以及用于求解所产生的三角系统的例程 xyyTRS[LAPACK99].

自适应阶数和工作量估计

为了自适应地在积分过程中改变外插法的阶数，有一个基本方案和外插序列所需的工作量的度量是重要的.

函数计算的相对代价的测量也是有好处的.

系统的维度，最好是带有根据结构的加权，需要与线性隐式方案相结合，以便于考虑求解每个线性系统的代价.

稳定性检验

外插法使用的一个大的基本步长可能会带来一些困难.

"因为溢出，没有代码可以简单求解 Van der Pol 方程问题..." [S87].

有两种稳定性检查用于线性隐式基本方案（进一步的讨论请参阅 [HW96] ).

一个检查是在外插过程中执行的. 令 .

为了在 的计算中终止计算，Deuflhard 建议检查应用于一个完全隐式方案的牛顿迭代是否收敛.

对于隐式欧拉方法，会产生如下的考虑：

请注意，(24) 与 (25) 只在第二个方程上不同. 它要求对一个不同的右边寻找解，但是没有额外的函数计算.

对于隐式中点法， 和 ，只简单地要求一些基本的算术操作.

增量是对于两种形式的稳定性检查的实现的一种更加准确的表述.

示例

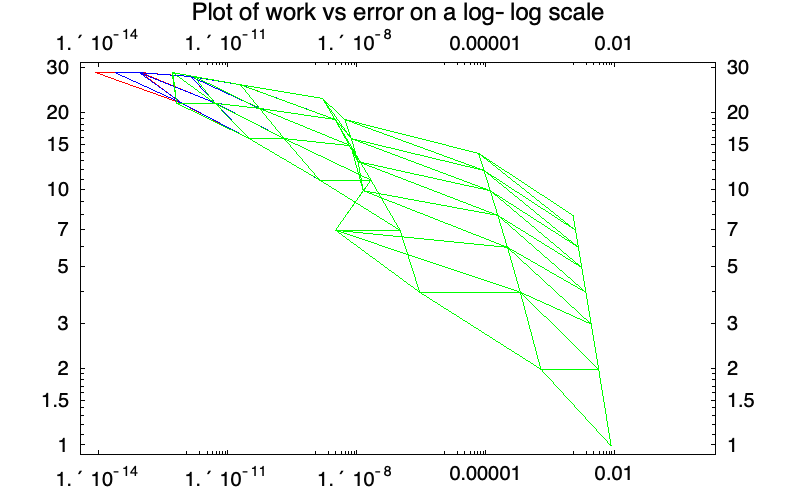
工作误差比较

精确解由 给出.

增量公式

本例子涉及带有调和序列的一个 "ExplicitEuler" 的八阶外插法. 通过在外插过程中使用基于增量的表述，我们获得到了将近两个数位的准确度.

• 标准表述 （26） 的结果用绿色描绘.

• 增量表述（27）后跟随标准外插法（2）的结果用蓝色描绘.

• 带有在使用（1）的增量上执行的外插法的增量表述（1）的结果用红色描绘.



通过在外插过程中使用基于增量的表述，获得将近两个小数位的准确度.

这里对前面例子中，形成外插表格的初始列的积分数据中的相对误差进行比较.

参考值使用具有32位小数位的软件算术进行计算，并且转换为最接近的IEEE双精度浮点数，其中一个 ULP 标志着在最后一位上的一个单位（Unit in the Last Place ）或者在最后的位置上的单位（Unit in the Last Position ）.



请注意，用于启迪舍入误差增长研究的舍入误差模型是有限的，因为在实践中， 中的误差可以超过 1 ULP.

在外插过程中使用的增量表述在 中产生比1 ULP 小的舍入误差.

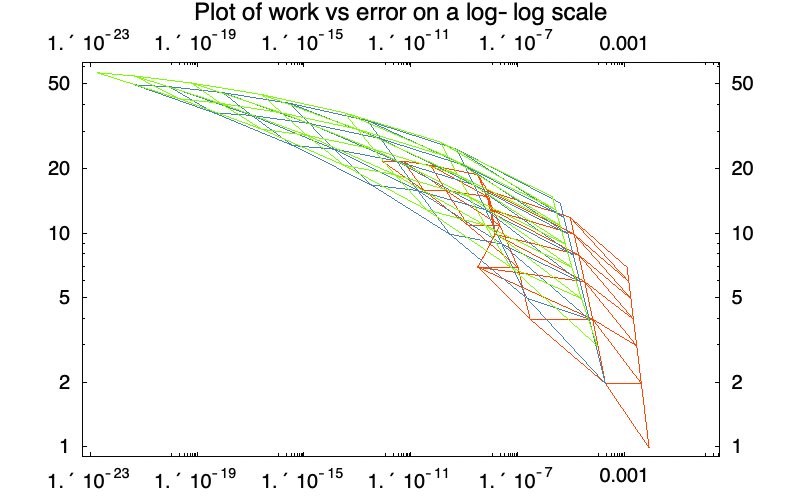
方法比较

下面对基于 "ExplicitEuler" （红色）、"ExplicitMidpoint" （蓝色）和 "ExplicitModifiedMidpoint" （绿色）的外插法所需的工作量进行比较.

所有的计算都使用具有32位小数位的软件算术执行.

阶数选择

方法比较

刚性系统

请注意，雅可比矩阵是自动计算的（可由用户通过使用数值差分或者符号导数来指定），适当的线性代数例程被选中，并且在运行时调用.

高精度比较

质量矩阵 - fem2ex

考虑偏微分方程：

给定一个整数 定义 并且在 采用 Galerkin 离散化近似，其中，：

其中 是一个分段线性函数，在 处是 而在 处是 .

适用于（1）的离散化（28）产生与（1）中相同的具有恒定质量矩阵公式的常微分方程组. 该常微分方程组是 [SR97] 中的fem2ex 问题，并且也可以在 IMSL 库中找到.

该问题的设置帮助我们对考虑小维度不是必需的矩阵使用稀疏阵列，但是如果离散化的点的数目增加，将具有良好的规模. 一个值为向量的变量用于初始条件. 该系统将在区间 上得到求解：

微调

"StepSizeSafetyFactors"

与绝大部分方法相同，我们需要在采取太小的步长和尝试大步长但是会频繁地被拒绝之间做出权衡. 如下所示，选项 "StepSizeSafetyFactors"->{s₁,s₂} 限制了步长的选择. 由阶数为 的方法选择的步长满足：

这里既包含一个与阶数相关的因子，也包含一个与阶数无关因子.

"StepSizeRatioBounds"

选项 "StepSizeRatioBounds"->{sr_min,sr_max} 指定采用的下一个步长的边界，使得：

"OrderSafetyFactors"

"Extrapolation" 中一个重要的方面是阶数选择.

每个外插步 都具有一个相关的工作量估计 .

对于显式基本方法的工作量估计是以函数计算的数目，和所采用的步序列为基础的.

线性隐式基本方法的工作量估计还包含计算雅可比的代价、一个LU分解的代价以及向后求解线性方程的代价的估计.

每个步骤的工作量估计是由对阶数为 的方法的工作量估计和所采用的期望新步长形成的（从（1）计算）： .

对连续的估计进行比较， 允许对什么时候一个不同的阶数方法更加有效做出决策.

选项 "OrderSafetyFactors"->{f₁,f₂} 指定在估计 的比较中所涉及的安全因子.

当 时降低阶数.

当 时增加阶数.

还有一些额外的限制，比如，当每步的最大阶数增加是1（对于对称方法，是2）的时候，和当在一个被拒步骤之后，阶数的增加被立即阻止的时候.

对于一个非刚性基本方法，默认值是 {4/5,9/10}，而对于一个刚性方法，它们是 {7/10,9/10}.

选项总结

选项名	默认值
"ExtrapolationSequence"	Automatic	指定在外插法中使用的序列
"MaxDifferenceOrder"	Automatic	指定使用的最大阶数
Method	"ExplicitModifiedMidpoint"	指定使用的基本积分方法
"MinDifferenceOrder"	Automatic	指定使用的最小阶数
"OrderSafetyFactors"	Automatic	指定自适应阶数选择的估计中所用的安全因子
"StartingDifferenceOrder"	Automatic	指定使用的初始阶数
"StepSizeRatioBounds"	Automatic	指定在新步长 上相对当前步长 变化的边界，即 low high
"StepSizeSafetyFactors"	Automatic	指定安全因子，用来结合进用于自适应步长的误差估计
"StiffnessTest"	Automatic	指定是否使用刚性检测功能

方法 "Extrapolation" 的选项.

选项 "ExtrapolationSequence" 的默认设置 Automatic 依据基本方法的刚性和对称性选择一个序列.

选项 "MaxDifferenceOrder" 的默认设置 Automatic 用十进制工作精度的两倍界定最大阶数.

选项 "MinDifferenceOrder" 的默认设置 Automatic 从基本方法的阶数开始，选择两种外插法的最小数目. 这也取决于基本方法是否是对称的.

选项 "OrderSafetyFactors" 的默认设置 Automatic 对一个刚性基本方法使用值 {7/10,9/10} 而对于一个非刚性基本方法使用 {4/5,9/10}.

选项 "StartingDifferenceOrder" 的默认设置 Automatic 取决于 "MinDifferenceOrder" 的设置 . 根据基本方法是否对称，它被设置为 或者 .

选项 "StepSizeRatioBounds" 的默认设置 Automatic 对一个刚性基本方法使用值 {1/10,4} 而对于一个非刚性基本方法使用 {1/50,4}.

选项 "StepSizeSafetyFactors" 的默认设置 Automatic 对于一个刚性基本方法使用值 {9/10,4/5} 而对于一个非刚性基本方法使用 {9/10,13/20}.

选项 "StiffnessTest" 的默认设置 Automatic 表明，如果使用非刚性基本方法，则刚性检测被激活.

方法 "LinearlyImplicitEuler"、"LinearlyImplicitMidpoint" 和 "LinearlyImplicitModifiedMidpoint" 的选项.