WOLFRAM SYSTEM MODELER
MichaelisMentenComparison between a rection under Michaelis-Menten reaction kinetics and a reaction using mass-action equations. |
|
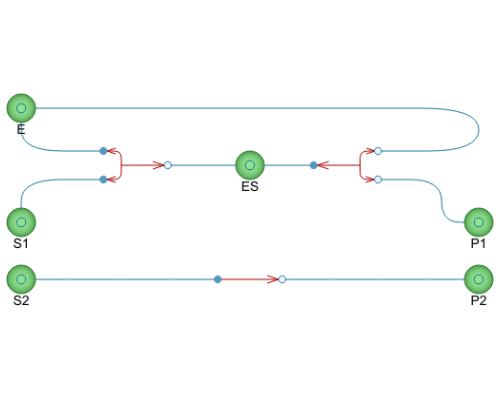
Diagram
Wolfram Language

SystemModel["EducationExamples.ComputationalBiology.MichaelisMenten"]
Information
Library Dependency
This model requires the BioChem library.
- The free BioChem library is an extendable, general purpose Modelica library for modeling, simulation and visualization of biological and biochemical systems. The library is designed to be used together with Wolfram System Modeler, which enables several extra features such as Systems Biology Markup Language (SBML) import and export. BioChem can, for instance, be used for selecting drug targets with PK/PD modeling or searching for novel drug targets with mechanistic modeling of the reactions in a cell or organism.
Model
This model studies the Michaelis–Menten kinetics and compares it to a standard, enzyme-catalyzed mass action reaction.
Michaelis–Menten kinetics is one of the most important models for enzyme-substrate interactions. It is used to study the kinetics in a wide array of biological functions, such as the immune response.
While a mass action model of an enzyme-substrate interaction would go through a intermediate step with an enzyme-substrate complex, Michealis–Menten kinetics assumes that this complex rapidly enters quasi steady state and can be approximated. This eliminates the need to measure the formation rate of this complex, which is infeasible in practice.
The example model consists of two separate reaction models. The upper, larger model follows mass action kinetics, having an enzyme that binds to the substrate, creating an enzyme-substrate complex before transforming the substrate into product. The smaller model follows Michaelis–Menten kinetics, with its reaction rate formula representing the enzyme reaction seen in the mass action model.
Simulation
Simulating the model will give the possibility to see how well the Michaelis–Menten model agrees with the mass action one (which is more biologically correct).
Simulate the model by clicking the Simulate button:
If the models do not seem to agree, try to increase the kCat constant, which represents the product formation from the enzyme-substrate complex. The higher the kCat, the better the models should agree. You can also change other parameters and initial conditions. This can be done in the Parameters tab. Change the corresponding initial concentration and then click the Simulate button again.
In order to get the full experience of this example, you need a desktop Wolfram Language product. A free trial download is available at www.wolfram.com/mathematica/trial/
For the full example, open the accompanying notebook MichaelisMenten.nb.
Parameters (8)
| mainCompartment |
Value: false Type: Boolean Description: Specifies whether the compartment is a main (top-level) compartment. Used in SBML import/export. |
|---|---|
| kOn |
Value: 2 Type: Real Description: Association constant for enzyme-substrate binding reaction |
| kOff |
Value: 4 Type: Real Description: Disassociation constant for enzyme-substrate binding reaction |
| kCat |
Value: 0.5 Type: Real Description: Reaction rate constant for enzyme reaction |
| Sc0 |
Value: 0.01 Type: Concentration (mol/l) Description: Initial concentration of substrate |
| Pc0 |
Value: 0 Type: Concentration (mol/l) Description: Initial concentration of product |
| Ec0 |
Value: 0.05 Type: Concentration (mol/l) Description: Initial concentration of enzymes |
| enzymeInitialization |
Value: MichaelisMenten.Init.Zero Type: Init Description: Initialization options for the enzyme reaction, see documentation |
Components (9)
| uui1 |
Type: Uui Description: The Michaelis-Menten reaction. |
|
|---|---|---|
| E |
Type: Substance Description: The enzyme provide a lower energy reaction path for the reaction by stabilizing the transition state, greatly increasing the reaction rate. |
|
| S1 |
Type: Substance Description: Substrate, which is defined as a reactant that is consumed in a enzymatic (or catalytic) reaction. |
|
| S2 |
Type: Substance Description: Substrate, which is defined as a reactant that is consumed in a enzymatic (or catalytic) reaction. |
|
| bur |
Type: Bur Description: The reversible, first reaction in the short reaction chain from substrate to product. |
|
| ES |
Type: Substance Description: The enzyme-substrate complex. The enzyme reversibly binds the substrate, stabilizing its transition state. |
|
| P1 |
Type: Substance Description: The resulting substance of the reaction. |
|
| P2 |
Type: Substance Description: The resulting substance of the reaction. |
|
| ubr |
Type: Ubr Description: The last reaction of the short chain from substrate to product. The forward rate is controlled by the kCat constant. |