WOLFRAM SYSTEM MODELER
lowPassReturn low pass filter roots as needed for block for given cut-off frequency |
|
Wolfram Language
SystemModel["Modelica.Blocks.Continuous.Internal.Filter.roots.lowPass"]
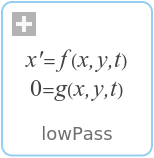
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
The goal is to implement the filter in the following form:
// real pole:
der(x) = r*x - r*u
y = x
// complex conjugate poles:
der(x1) = a*x1 - b*x2 + ku*u;
der(x2) = b*x1 + a*x2;
y = x2;
ku = (a^2 + b^2)/b
This representation has the following transfer function:
// real pole:
s*y = r*y - r*u
or
(s-r)*y = -r*u
or
y = -r/(s-r)*u
comparing coefficients with
y = cr/(s + cr)*u -> r = -cr // r is the real eigenvalue
// complex conjugate poles
s*x2 = a*x2 + b*x1
s*x1 = -b*x2 + a*x1 + ku*u
or
(s-a)*x2 = b*x1 -> x2 = b/(s-a)*x1
(s + b^2/(s-a) - a)*x1 = ku*u -> (s(s-a) + b^2 - a*(s-a))*x1 = ku*(s-a)*u
-> (s^2 - 2*a*s + a^2 + b^2)*x1 = ku*(s-a)*u
or
x1 = ku*(s-a)/(s^2 - 2*a*s + a^2 + b^2)*u
x2 = b/(s-a)*ku*(s-a)/(s^2 - 2*a*s + a^2 + b^2)*u
= b*ku/(s^2 - 2*a*s + a^2 + b^2)*u
y = x2
comparing coefficients with
y = c0/(s^2 + c1*s + c0)*u -> a = -c1/2
b = sqrt(c0 - a^2)
ku = c0/b
= (a^2 + b^2)/b
comparing with eigenvalue representation:
(s - (a+jb))*(s - (a-jb)) = s^2 -2*a*s + a^2 + b^2
shows that:
a: real part of eigenvalue
b: imaginary part of eigenvalue
time -> infinity:
y(s=0) = x2(s=0) = 1
x1(s=0) = -ku*a/(a^2 + b^2)*u
= -(a/b)*u
Syntax
Inputs (4)
| cr_in |
Type: Real[:] Description: Coefficients of real poles of base filter |
|---|---|
| c0_in |
Type: Real[:] Description: Coefficients of s^0 term of base filter if conjugate complex pole |
| c1_in |
Type: Real[size(c0_in, 1)] Description: Coefficients of s^1 term of base filter if conjugate complex pole |
| f_cut |
Type: Frequency (Hz) Description: Cut-off frequency |
Outputs (4)
| r |
Type: Real[size(cr_in, 1)] Description: Real eigenvalues |
|---|---|
| a |
Type: Real[size(c0_in, 1)] Description: Real parts of complex conjugate eigenvalues |
| b |
Type: Real[size(c0_in, 1)] Description: Imaginary parts of complex conjugate eigenvalues |
| ku |
Type: Real[size(c0_in, 1)] Description: Input gain |
