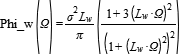WOLFRAM SYSTEM MODELER
DrydenContinuousTurbulenceDemonstrates how to model wind turbulence for aircraft with the BandLimitedWhiteNoise block (a simple model of vertical Dryden gust speed at low altitudes < 1000 ft) |
|
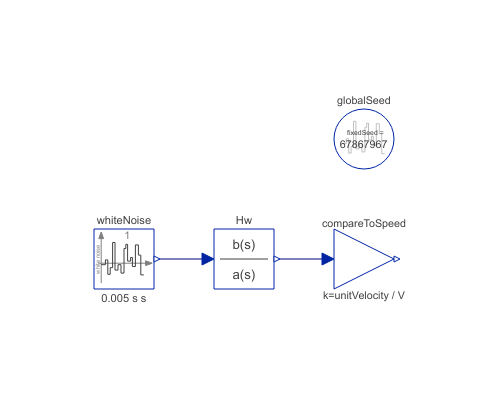
Diagram
Wolfram Language
SystemModel["Modelica.Blocks.Examples.NoiseExamples.DrydenContinuousTurbulence"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
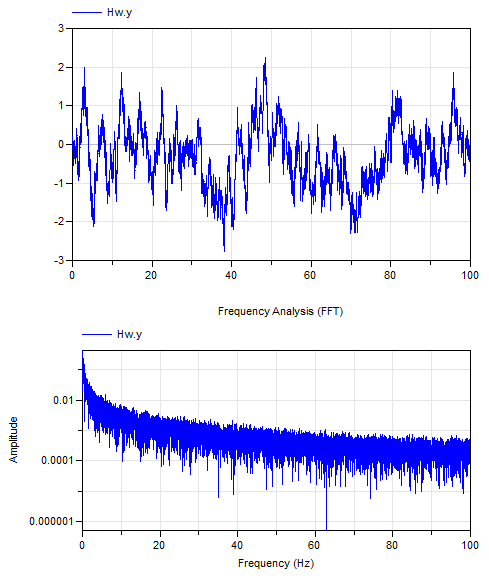
This example shows how to use the BandLimitedWhiteNoise to feed a Dryden continuous turbulence model. This model is used to describe turbulent wind at low altitudes that varies randomly in space (see also wikipedia).
Turbulence model for vertical gust speed at low altitudes
The turbulence model of the Dryden form is defined by the power spectral density of the vertical turbulent velocity:
The spectrum is parametrized with the following parameters:
- Lw is the turbulence scale.
In low altitudes, it is equal to the flight altitude. - sigma is the turbulence intensity.
In low altitudes, it is equal to 1/10 of the wind speed at 20 ft altitude, which is 30 kts for medium turbulence. - Omega is the spatial frequency.
The turbulence model is thus defined in space and the aircraft experiences turbulence as it flies through the defined wind field. - Omega = s/V will be used to transform the spatial definition into a temporal definition, which can be realized as a state space system.
- V is the airspeed of the aircraft.
It is approximately 150 kts during the approach (i.e. at low altitudes).
Using spectral factorization and a fixed airspeed V of the aircraft, a concrete forming filter for the vertical turbulence can be found as
,
for which V * (H_w(i Omega/V) * H_w(-i Omega/V) = Phi_w(Omega).
The input to the filter
The input to the filter is white noise with a normal distribution, zero mean, and a power spectral density of 1. That means, for a sampling time of 1s, it is parameterized with mean=0 and variance=1. However, in order to account for the change of noise power due to sampling, the noise must be scaled with sqrt(samplePeriod). This is done automatically in the BandLimitedWhiteNoise block.
Example output
Reference
- Dryden Wind Turbulence model in US military standard MIL-F-8785.
Parameters (3)
| V |
Value: 140 * 0.5144 Type: Velocity (m/s) Description: Airspeed of aircraft (typically 140kts during approach) |
|---|---|
| sigma |
Value: 0.1 * 30 * 0.5144 Type: Velocity (m/s) Description: Turbulence intensity (=0.1 * wind at 20 ft, typically 30 kt) |
| L |
Value: 600 * 0.3048 Type: Length (m) Description: Scale length (= flight altitude) |
Components (4)
| Hw |
Type: TransferFunction Description: Transfer function of vertical turbulence speed according to MIL-F-8785C |
|
|---|---|---|
| whiteNoise |
Type: BandLimitedWhiteNoise |
|
| compareToSpeed |
Type: Gain |
|
| globalSeed |
Type: GlobalSeed |