WOLFRAM SYSTEM MODELER
UniformNoisePropertiesDemonstrates the computation of properties for uniformally distributed noise |
|
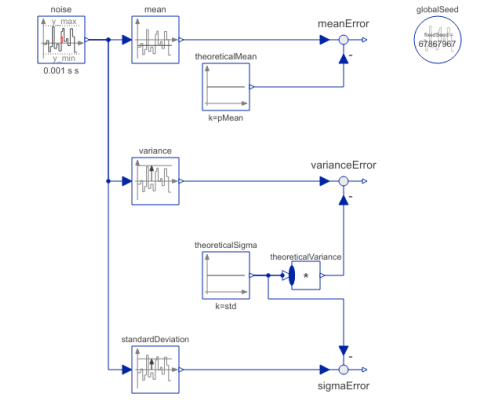
Diagram
Wolfram Language
SystemModel["Modelica.Blocks.Examples.NoiseExamples.UniformNoiseProperties"]
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
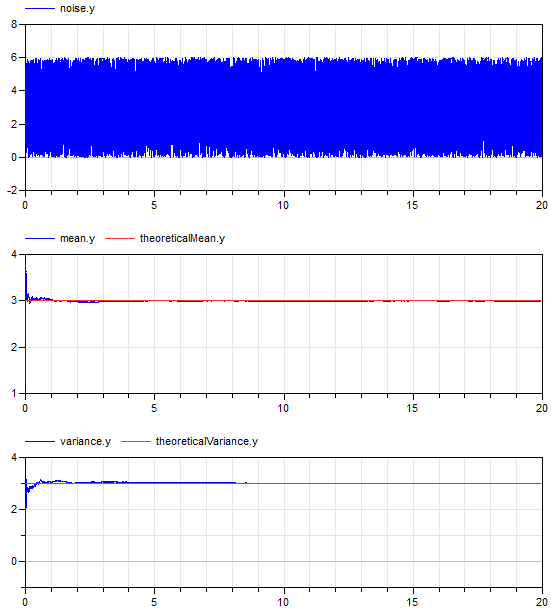
This example demonstrates statistical properties of the Blocks.Noise.UniformNoise block using a uniform random number distribution. Block "noise" defines a band of 0 .. 6 and from the generated noise the mean and the variance is computed with blocks of package Blocks.Math. Simulation results are shown in the next diagram:
The mean value of a uniform noise in the range 0 .. 6 is 3 and its variance is 3 as well. The simulation results above show good agreement (after a short initial phase). This demonstrates that the random number generator and the mapping to a uniform distribution have good statistical properties.
Parameters (5)
| y_min |
Value: 0 Type: Real Description: Minimum value of band |
|---|---|
| y_max |
Value: 6 Type: Real Description: Maximum value of band |
| pMean |
Value: (y_min + y_max) / 2 Type: Real Description: Theoretical mean value of uniform distribution |
| var |
Value: (y_max - y_min) ^ 2 / 12 Type: Real Description: Theoretical variance of uniform distribution |
| std |
Value: sqrt(var) Type: Real Description: Theoretical standard deviation of uniform distribution |
Outputs (2)
| meanError_y |
Default Value: meanError.y Type: Real |
|---|---|
| sigmaError_y |
Default Value: sigmaError.y Type: Real |
Components (11)
| globalSeed |
Type: GlobalSeed |
|
|---|---|---|
| noise |
Type: UniformNoise |
|
| mean |
Type: ContinuousMean |
|
| variance |
Type: Variance |
|
| theoreticalVariance |
Type: MultiProduct |
|
| meanError |
Type: Feedback |
|
| theoreticalMean |
Type: Constant |
|
| varianceError |
Type: Feedback |
|
| theoreticalSigma |
Type: Constant |
|
| standardDeviation |
Type: StandardDeviation |
|
| sigmaError |
Type: Feedback |
Revisions
| Date | Description | ||
|---|---|---|---|
| June 22, 2015 |
|