WOLFRAM

WOLFRAM SYSTEM MODELER

norm

Returns the p-norm of a complex vector

Wolfram Language

In[1]:=
SystemModel["Modelica.ComplexMath.Vectors.norm"]
Out[1]:=

Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

Syntax

Vectors.norm(v);
Vectors.norm(v,p=2);   // 1 ≤ p ≤ ∞

Description

The function call "Vectors.norm(v)" returns the Euclidean norm "sqrt(v*v)" of vector v. With the optional second argument "p", any other p-norm can be computed:

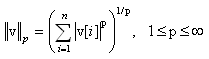
function Vectors.norm

Besides the Euclidean norm (p=2), also the 1-norm and the infinity-norm are sometimes used:

1-norm = sum(abs(v)) norm(v,1)
2-norm = sqrt(v*v) norm(v) or norm(v,2)
infinity-norm = max(abs(v)) norm(v,Modelica.Constants.inf)

Note, for any vector norm the following inequality holds: 

norm(v1+v2,p) ≤ norm(v1,p) + norm(v2,p)

Example

v = {2, -4, -2, -1};
norm(v,1);    // = 9
norm(v,2);    // = 5
norm(v);      // = 5
norm(v,10.5); // = 4.00052597412635
norm(v,Modelica.Constants.inf);  // = 4

See also

Matrices.norm

Syntax

result = norm(v, p)

Inputs (2)

v

Type: Complex[:]

Description: Vector
p

Default Value: 2

Type: Real

Description: Type of p-norm (often used: 1, 2, or Modelica.Constants.inf)

Outputs (1)

result

Type: Real

Description: p-norm of vector v