This information is part of the Modelica Standard Library maintained by the Modelica Association.

In polyphase systems, the angular displacement of voltages and currents of the phases as well as the spatial displacement of machine windings have to follow the same rules, i.e., they are based on the same orientation function.

Symmetrical three-phase system

A symmetrical three-phases system consists of three sinusoidal sine waves with an angular displacement of 2 π / 3.

Symmetrical polyphase system

In symmetrical polyphase systems odd and even phase numbers have to be distinguished.

Odd number of phases

For a symmetrical polyphase system with m phases the displacement of the sine waves is 2 π / m.

Fig. 1: Symmetrical (a) three-phase and (b) five-phase current system

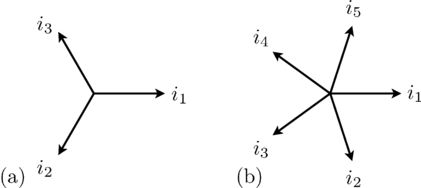
Even number of phases

In case of an even number of phases the aligned orientation does not add any information. Instead the m phases are divided into two or more different groups (the base systems).

The number of phases m can be divided by 2 recursively until the result is either an odd number or 2. The result of this division is called m_Base, the number of phases of the base system. The number of base systems n_Base is defined by the number of divisions, i.e., m = n_Base * m_Base.

For a base system with m_Base phases the displacement of the sine waves belonging to that base system is 2 π / m_Base.

Fig. 2: Symmetrical (a) six and (b) ten phase current system

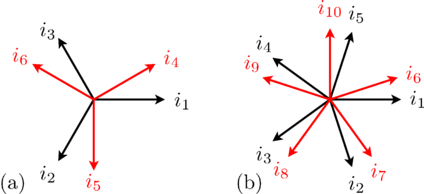
The displacement of the base systems is defined as π / n_Base.

Note

In array or matrices, the base systems are stored one after another.

Symmetrical components

For each base system of time phasors, symmetrical components can be calculated according to the idea of Charles L. Fortescue.

The first symmetrical component is the direct component with positive sequence.
In case of m_Base = 2, the second component is the inverse component with negative sequence.
In case of m_Base > 2, the components [2..m_Base - 1] are components with non-positive sequence,
and the last component [m_Base] is the zero sequence component.

This set of symmetrical components is repeated for each of the n_Base base systems.

Polygon connection

For polyphase systems, star connection of the m phases is unambiguous, i.e., each pin of the plug is connected to the starpoint pin, whereas for polygon connection (m_Base - 1)/2 alternatives exist (refer to Fig. 3).

Fig. 3: Line-to-neutral voltages and line-to-line voltages for different systems

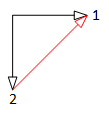
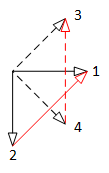
2 phase system	2 = 2 x 2 phase system
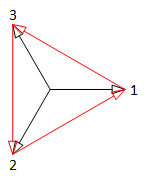
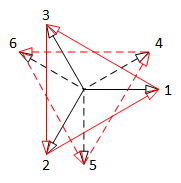
3 phase system	6 = 2 x 3 phase system
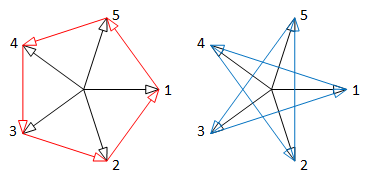
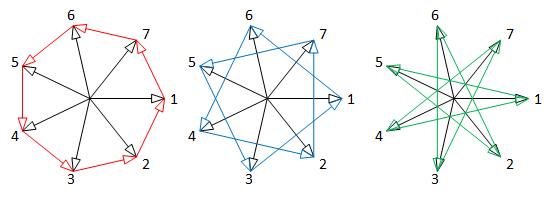
5 phase system: 2 alternative polygon connections	7 phase system: 3 alternative polygon connections

Therefore, using the MultiDelta component, the alternative has to be specified by the parameter kPolygon.

See also

User's guide on polyphase winding.