Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

The purely sinusoidal voltage

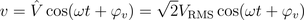
$v=\sqrt{2}V_{\mathrm{RMS}}\cos(\omega t+\varphi_{v})$

in the time domain can be represented by a complex rms phasor

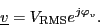
$\underline{v}=V_{\mathrm{RMS}}e^{j\varphi_{v}}.$

For these quasi-static phasor the following relationship applies:

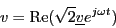
$\begin{displaymath} v=\mathrm{Re}(\sqrt{2}\underline{v}e^{j\omega t})\end{displaymath}$

This equation is also illustrated in Fig. 1.

Fig. 1: Relationship between voltage phasor and time domain voltage

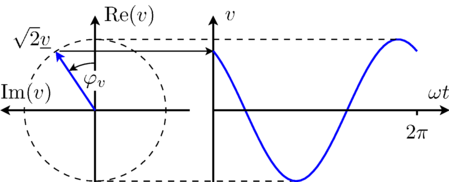
From the above equation it is obvious that for t = 0 the time domain voltage is v = cos(φ_v). The complex representation of the phasor corresponds with this instance, too, since the phasor is leading the real axis by the angle φ_v.

The explanation given for sinusoidal voltages can certainly also be applied to sinusoidal currents.

Introduction

Wolfram Language

Information

See also