WOLFRAM SYSTEM MODELER
regRoot2Anti-symmetric approximation of square root with discontinuous factor so that the first derivative is finite and continuous |
|
Wolfram Language

SystemModel["Modelica.Fluid.Utilities.regRoot2"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Approximates the function
y = if x ≥ 0 then sqrt(k1*x) else -sqrt(k2*abs(x)), with k1, k2 ≥ 0
in such a way that within the region -x_small ≤ x ≤ x_small, the function is described by two polynomials of third order (one in the region -x_small .. 0 and one within the region 0 .. x_small) such that
- The derivative at x=0 is finite.
- The overall function is continuous with a continuous first derivative everywhere.
- If parameter use_yd0 = false, the two polynomials are constructed such that the second derivatives at x=0 are identical. If use_yd0 = true, the derivative at x=0 is explicitly provided via the additional argument yd0. If necessary, the derivative yd0 is automatically reduced in order that the polynomials are strict monotonically increasing [Fritsch and Carlson, 1980].
Typical screenshots for two different configurations are shown below. The first one with k1=k2=1:
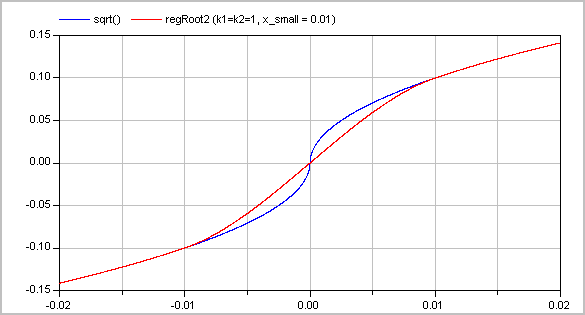
and the second one with k1=1 and k2=3:
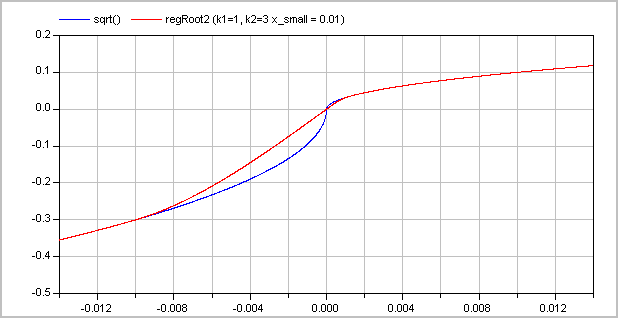
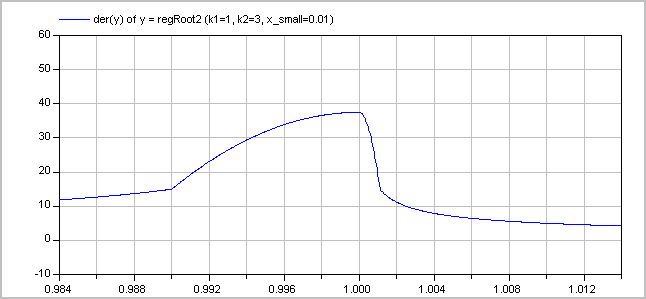
The (smooth) derivative of the function with k1=1, k2=3 is shown in the next figure:
Literature
- Fritsch F.N. and Carlson R.E. (1980):
- Monotone piecewise cubic interpolation. SIAM J. Numerc. Anal., Vol. 17, No. 2, April 1980, pp. 238-246
Syntax
Inputs (6)
| x |
Type: Real Description: Abscissa value |
|---|---|
| x_small |
Default Value: 0.01 Type: Real Description: Approximation of function for |x| <= x_small |
| k1 |
Default Value: 1 Type: Real Description: y = if x>=0 then sqrt(k1*x) else -sqrt(k2*|x|) |
| k2 |
Default Value: 1 Type: Real Description: y = if x>=0 then sqrt(k1*x) else -sqrt(k2*|x|) |
| use_yd0 |
Default Value: false Type: Boolean Description: = true, if yd0 shall be used |
| yd0 |
Default Value: 1 Type: Real Description: Desired derivative at x=0: dy/dx = yd0 |
Outputs (1)
| y |
Type: Real Description: Ordinate value |
|---|
Revisions
- Sept., 2010
by Martin Otter:
Improved so that k1=0 and/or k2=0 is also possible. - Nov., 2005
by Martin Otter:
Designed and implemented.
