WOLFRAM SYSTEM MODELER
quantileQuantile of truncated normal distribution |
|
Wolfram Language

SystemModel["Modelica.Math.Distributions.TruncatedNormal.quantile"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
Syntax
Normal.quantile(u, y_min=0, y_max=1, mu=0, sigma=1);
Description
This function computes the inverse cumulative distribution function (= quantile) according to a truncated normal distribution with minimum value u_min, maximum value u_max, mean value of original distribution mu and standard deviation of original distribution sigma (variance = sigma2). Input argument u must be in the range:
0 < u < 1
Output argument y is in the range:
y_min ≤ y ≤ y_max
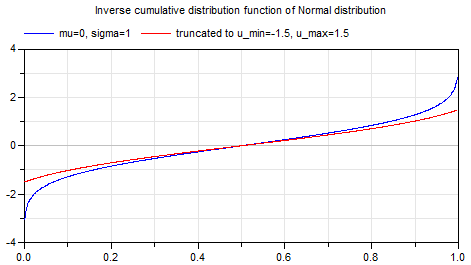
Plot of the function:
For more details
of the normal distribution, see
Wikipedia,
of truncated distributions, see
Wikipedia.
Example
quantile(0.001) // = 0.001087357613043849; quantile(0.5,0,1,0.5,0.9) // = 0.5
See also
Syntax
Inputs (5)
| u |
Type: Real Description: Random number in the range 0 <= u <= 1 |
|---|---|
| y_min |
Default Value: 0 Type: Real Description: Lower limit of y |
| y_max |
Default Value: 1 Type: Real Description: Upper limit of y |
| mu |
Default Value: (y_max + y_min) / 2 Type: Real Description: Expectation (mean) value of the normal distribution |
| sigma |
Default Value: (y_max - y_min) / 6 Type: Real Description: Standard deviation of the normal distribution |
Outputs (1)
| y |
Type: Real Description: Random number u transformed according to the given distribution |
|---|
Revisions
| Date | Description | ||
|---|---|---|---|
| June 22, 2015 |
|