WOLFRAM

WOLFRAM SYSTEM MODELER

Nonlinear

Library of functions operating on nonlinear equations

Package Contents

Examples

Examples demonstrating the usage of the functions in package Nonlinear

Interfaces

Interfaces for functions

quadratureLobatto

Return the integral of an integrand function using an adaptive Lobatto rule

solveOneNonlinearEquation

Solve f(u) = 0 in a very reliable and efficient way (f(u_min) and f(u_max) must have different signs)

Information

This information is part of the Modelica Standard Library maintained by the Modelica Association.

This package contains functions to perform tasks such as numerically integrating a function, or solving a nonlinear algebraic equation system. The common feature of the functions in this package is that the nonlinear characteristics are passed as user definable functions.

For details about how to define and to use functions as input arguments to functions, see ModelicaReference.Classes.'function' or Section 12.4.2 (Functional Input Arguments to Functions) of the Modelica 3.4 specification.

Wolfram Language

In[1]:=
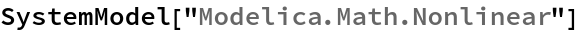
SystemModel["Modelica.Math.Nonlinear"]
Out[1]:=

Revisions

  • July 2010 by Martin Otter (DLR-RM):
    Included in MSL 3.2, adapted, and documentation improved
  • March 2010 by Andreas Pfeiffer (DLR-RM):
    Adapted the quadrature function from Gerhard Schillhuber and the solution of one non-linear equation in one unknown from Modelica.Media.Common.OneNonLinearEquation so that function objects are used.
  • June 2002 by Gerhard Schillhuber (master thesis at DLR-RM):
    Adaptive quadrature to compute the curve length of a Spline.