WOLFRAM SYSTEM MODELER
solveSolve f_nonlinear(x_zero)=y_zero; f_nonlinear(x_min) - y_zero and f_nonlinear(x_max)-y_zero must have different sign |
|
Wolfram Language
SystemModel["Modelica.Media.Common.OneNonLinearEquation.solve"]
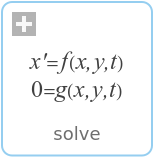
Syntax
Inputs (7)
| y_zero |
Type: Real Description: Determine x_zero, such that f_nonlinear(x_zero) = y_zero |
|---|---|
| x_min |
Type: Real Description: Minimum value of x |
| x_max |
Type: Real Description: Maximum value of x |
| pressure |
Default Value: 0.0 Type: Real Description: Disregarded variables (here always used for pressure) |
| X |
Default Value: fill(0, 0) Type: Real[:] Description: Disregarded variables (here always used for composition) |
| f_nonlinear_data |
Type: f_nonlinear_Data Description: Additional data for function f_nonlinear |
| x_tol |
Default Value: 100 * Modelica.Constants.eps Type: Real Description: Relative tolerance of the result |
Outputs (1)
| x_zero |
Type: Real Description: f_nonlinear(x_zero) = y_zero |
|---|
Extended by (8)
|
Modelica.Media.IdealGases.Common.MixtureGasNasa.T_psX.Internal |
|
|
Modelica.Media.IdealGases.Common.MixtureGasNasa.T_hX.Internal |
|
|
Modelica.Media.IdealGases.Common.SingleGasNasa.T_ps.Internal |
|
|
Modelica.Media.IdealGases.Common.SingleGasNasa.T_h.Internal |
|
|
Modelica.Media.Air.MoistAir.T_psX.Internal |
|
|
Modelica.Media.Air.MoistAir.T_phX.Internal |
|
|
Modelica.Media.Air.MoistAir.saturationTemperature.Internal |
|
|
Modelica.Media.Examples.SolveOneNonlinearEquation.Inverse_sine.Inverse_sine_definition Solution algorithm of non-linear equation |
