WOLFRAM SYSTEM MODELER
SpecificEnthalpyAsFunctionSpecific enthalpy as function |
|
Wolfram Language

SystemModel["Modelica.Media.UsersGuide.MediumDefinition.SpecificEnthalpyAsFunction"]

Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
If pressure p and specific enthalpy h are not used as independent medium variables, the specific enthalpy should be computed by a Modelica function that has as input arguments only the independent medium variables. It should not be computed by an equation. For example, if p and T are used as independent medium variables, a function h_pT(p,T) should be defined that is called to compute h:
h = h_pT(p,T);
The reason for this rule requires a longer explanation. In short, if h is not a computed by a Modelica function and this function is non-linear in the independent medium variables, then non-linear systems of equations will occur at every connection point, if the FluidPort connectors from the Modelica.Fluid library are used (these are the same as in Modelica.Media.Examples.Utilities.FluidPort). Only, if the above rule is fulfilled, a tool is able to remove these non-linear system of equations in most cases.
The basic idea of the FluidPort connector is that 2 or more components can be connected together at a point and that automatically the mass and energy balance is fulfilled in the connection point, i.e., the ideal mixing equations are generated. Note, the momentum balance is only correct for straight line connections. If "ideal mixing" is not sufficient, a special component to define the mixing equations must be introduced.
The mass and momentum balance equations in a component are derived from the partial differential equations along the flow direction of a pipe:
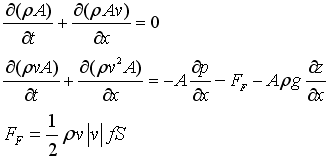
Note, FF is the fanning friction factor. The energy balance can be given in different forms. Usually, it is given as:
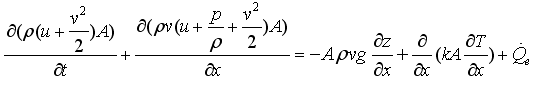
This form describes the change of the internal energy, kinetic energy and potential energy of a volume as function of the in and out flowing fluid. Multiplying the momentum balance with the flow velocity v and subtracting it from the energy balance above, results in the following alternative form of the energy balance:
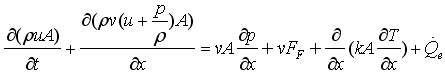
This form has the advantage that the kinetic and potential energy is no longer part of the energy balance and therefore the energy balance is substantially simpler (e.g., additional non-linear systems of equations occur in the first form since the velocity is present in the energy balance; in the second form this is not the case and it is still valid also for high speeds).
Assume now that the second form of the energy balance above is used in all components and that the following FluidPort connector is used in all components:
connector FluidPort replaceable package Medium = Modelica.Media.Interfaces.PartialMedium; Medium.AbsolutePressure p; flow Medium.MassFlowRate m_flow; Medium.SpecificEnthalpy h; flow Medium.EnthalpyFlowRate H_flow; Medium.MassFraction Xi [Medium.nXi]; flow Medium.MassFlowRate mX_flow[Medium.nXi]; end FluidPort;
As an example, assume that 3 components are connected together and that the medium is a single substance fluid. This will result in the following connection equations:
p1=p2=p3; h1=h2=h3; 0 = m_flow1 + m_flow2 + m_flow3; 0 = H_flow1 + H_flow2 + H_flow3;
These are the mass balance and the energy balance (form 2) of an infinitesimal volume in the connection point under the assumption that no mass or energy is stored in this volume. In other words, the connection equations are the equations that describe ideal mixing. Under the assumption that the velocity vectors of the 3 flows are identical (especially, they are parallel), also the momentum balance is fulfilled:
0 = m_flow1*v1 + m_flow2*v2 + m_flow3*v3; = v*(m_flow1 + m_flow2 + m_flow3); = 0;
With the above connector it is therefore possible to connect components together in a nearly arbitrary fashion, because every connection fulfills automatically the balance equations. This approach has, however, one drawback: If two components are connected together, then the medium variables on both sides of the connector are identical. However, due to the connector, only the two equations
p1 = p2; h1 = h2;
are present. Assume, that p,T are the independent medium variables and that the medium properties are computed at one side of the connections. This means, the following equations are basically present:
h1 = h(p1,T1); h2 = h(p2,T2); p1 = p2; h1 = h2;
These equations can be solved in the following way:
h1 := h(p1,T1) p2 := p1; h2 := h1; 0 := h2 - h(p2,T2); // non-linear system of equations for T2
This means that T2 is computed by solving a non-linear system of equations. If h1 and h2 are provided as Modelica functions, a Modelica translator can replace this non-linear system of equations by the equation:
T2 := T1;
because after alias substitution there are two function calls
h1 := h(p1,T1); h1 := h(p1,T2);
Since the left hand side of the function call and the first argument are the same, the second arguments T1 and T2 must also be identical and therefore T2 := T1. This type of analysis seems to be only possible, if the specific enthalpy is defined as a function of the independent medium variables.
