This information is part of the Modelica Standard Library maintained by the Modelica Association.

In this section, an overview of the most important features of this library is given.

Steps and Transitions

A StateGraph is an enhanced finite state machine. It is based on the JGrafchart method and takes advantage of Modelica features for the "action" language. JGrafchart is a further development of Grafcet to include elements of StateCharts that are not present in Grafcet/Sequential Function Charts. Therefore, the StateGraph library has a similar modeling power as StateCharts but avoids some deficiencies of StateCharts.

The basic elements of StateGraphs are steps and transitions:

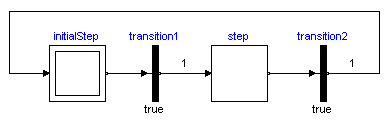
Steps represent the possible states a StateGraph can have. If a step is active the Boolean variable active of the step is true. If it is deactivated, active = false. At the initial time, all "usual" steps are deactivated. The InitialStep objects are steps that are activated at the initial time. They are characterized by a double box (see figure above).

Transitions are used to change the state of a StateGraph. When the step connected to the input of a transition is active, the step connected to the output of this transition is deactivated and the transition condition becomes true, then the transition fires. This means that the step connected to the input to the transition is deactivated and the step connected to the output of the transition is activated.

The transition condition is defined via the parameter menu of the transition object. Clicking on object "transition1" in the above figure, results in the following menu:

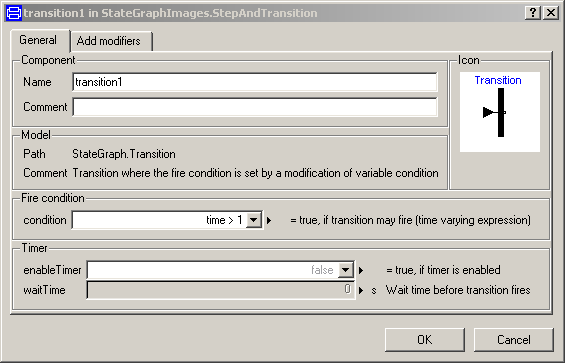
In the input field "condition", any type of time varying Boolean expression can be given (in Modelica notation, this is a modification of the time varying variable condition). Whenever this condition is true, the transition can fire. Additionally, it is possible to activate a timer, via enableTimer (see menu above) and provide a waitTime. In this case the firing of the transition is delayed according to the provided waitTime. The transition condition and the waitTime are displayed in the transition icon.

In the above example, the simulation starts at initialStep. After 1 second, transition1 fires and step1 becomes active. After another second transition2 fires and initialStep becomes again active. After a further second step1 becomes again active, and so on.

In JGrafcharts, Grafcet and Sequential Function Charts, the network of steps and transitions is drawn from top to bottom. In StateGraphs, no particular direction is defined, since steps and transitions are blocks with input and output connectors that can be arbitrarily placed and connected. Usually, it is most practical to define the network from left to right, as in the example above, since then it is easy to read the labels on the icons.

Conditions and Actions

With the block TransitionWithSignal, the firing condition can be provided as Boolean input signal, instead as entry in the menu of the transition. An example is given in the next figure:

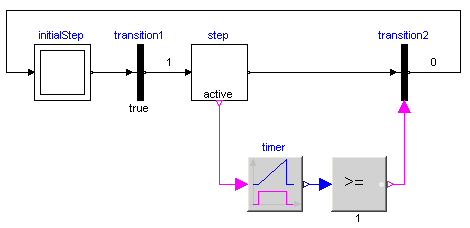
Component "step" is an instance of "StepWithSignal" that is a usual step where the active flag is available as Boolean output signal. To this output, component "Timer" from library "Modelica.Blocks.Logical" is connected. It measures the time from the time instant where the Boolean input (i.e., the active flag of the step) became true up to the current time instant. The timer is connected to a comparison component. The output is true, once the timer reaches 1 second. This signal is used as condition input of the transition. As a result, "transition2" fires, once step "step" has been active for 1 second. Of course, any other Modelica block with a Boolean output signal can be connected to the condition input of such a transition block as well.

Conditions of a transition can either be computed by a network of logical blocks from the Logical library as in the figure above, or via the "SetBoolean" component any type of logical expression can be defined in textual form, as shown in the next figure:

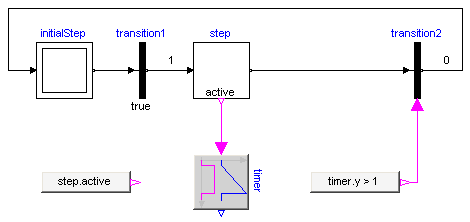
With the block "SetBoolean", a time varying expression can be provided as modification to the output signal y (see block with icon text "timer.y > 1" in the figure above). The output signal can be in turn connected to the condition input of a TransitionWithSignal block.

The "SetBoolean" block can also be used to compute a Boolean signal depending on the active step. In the figure above, the output of the block with the icon text "step.active" is true, when "step" is active, otherwise it is false (note, the icon text of "SetBoolean" displays the modification of the output signal "y"). This signal can then be used to compute desired actions in the physical systems model. For example, if a valve shall be open, when the StateGraph is in "step1" or in "step4", a "SetBoolean" block may be connected to the valve model using the following condition:

valve = step1.active or step2.active

Via the Modelica operators edge(..) and change(..), conditions depending on rising and falling edges of Boolean expressions can be used when needed.

In JGrafcharts, Grafcet, Sequential Function Charts and StateCharts, actions are formulated within a step. Such actions are distinguished as entry, normal, exit and abort actions. For example, a valve might be opened by an entry action of a step and might be closed by an exit action of the same step. In StateGraphs, this is (fortunately) not possible due to Modelica's "single assignment rule" that requires that every variable is defined by exactly one equation. Instead, the approach explained above is used. For example, via the "SetBoolean" component, the valve variable is set to true when the StateGraph is in particular steps.

This feature of a StateGraph is very useful, since it allows a Modelica translator to guarantee that a given StateGraph has always deterministic behaviour without conflicts. In the other methodologies this is much more cumbersome. For example, if two steps are executed in parallel and both step actions modify the same variable, the result is either non-deterministic or non-obvious rules have to be defined which action takes priority. In a StateGraph, such a situation is detected by the translator resulting in an error, since there are two equations to compute one variable. Additional benefits of the StateGraph approach are:

• A JGrafchart or a StateChart need to potentially access variables in a step that are defined in higher hierarchical levels of a model. Therefore, mostly global variables are used in the whole network, even if the network is structured hierarchically. In StateGraphs this is not necessary, since the physical systems outside of a StateGraph might access the step or transition state via a hierarchical name. This means that no global variables are needed, because the local variables in the StateGraph are accessed from local variables outside of the StateGraph.
• It is simpler for a user to understand the information that is provided in the non-graphical definition, since every variable is defined at exactly one place. In the other methodologies, the setting and re-setting of the same variable is cluttered within the whole network.

To emphasize this important difference between these methodologies, consider the case that a state machine has the following hierarchy:

stateMachine.superstate1.superstate2.step1

Within "step1" a StateChart would, e.g., access variable "stateMachine.openValve", say as "entry action: openValve = true". This typical usage has the severe drawback that it is not possible to use the hierarchical state "superstate1" as component in another context, because "step1" references a particular name outside of this component.

In a StateGraph, there would be typically a "SetBoolean" component in the "stateMachine" component stating:

openValve = superstate1.superstate2.step1.active;

As a result, the "superstate1" component can be used in another context, because it does not depend on the environment where it is used.

Execution Model

The execution model of a StateGraph follows from its Modelica implementation: Given the states of all steps, i.e., whether a step is active or not active, the equations of all steps, transitions, transition conditions, actions etc. are sorted resulting in an execution sequence to compute essentially the new values of the steps. If conflicts occur, e.g., if there are more equations as variables, of if there are algebraic loops between Boolean variables, an exception is raised. Once all equations have been processed, the active variables of all steps are updated to the newly calculated values. Afterwards, the equations are again evaluated. The iteration stops, once no step changes its state anymore, i.e., once no transition fires anymore. Then, simulation continuous until a new event is triggered, (when a relation changes its value).

With the Modelica "sample(..)" operator, a StateGraph might also be executed within a discrete controller that is called at regular time instants. Furthermore, clocked state machines are directly supported by the Modelica language itself, see Section 17 (State Machines) of the Modelica 3.4 specification.

Parallel and Alternative Execution

Parallel activities can be defined by component Parallel and alternative activities can be defined by component Alternative. An example for both components is given in the next figure.

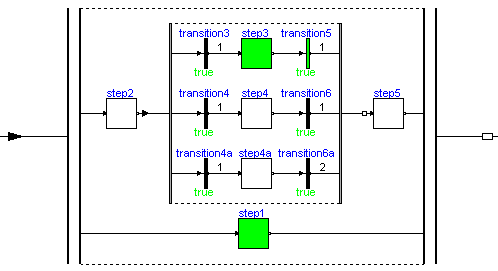
Here, the branch from "step2" to "step5" is executed in parallel to "step1". A transition connected to the output of a parallel branch component can only fire if the final steps in all parallel branches are active simultaneously. The figure above is a screen-shot from the animation of the StateGraph: Whenever a step is active or a transition can fire, the corresponding component is marked in green color.

The three branches within "step2" to "step5" are executed alternatively, depending which transition condition of "transition3", "transition4", "transition4a" fires first. Since all three transitions fire after 1 second, they are all candidates for the active branch. If two or more transitions would fire at the same time instant, a priority selection is made: The alternative and parallel components have a vector of connectors. Every branch has to be connected to exactly one entry of the connector vector. The entry with the lowest number has the highest priority.

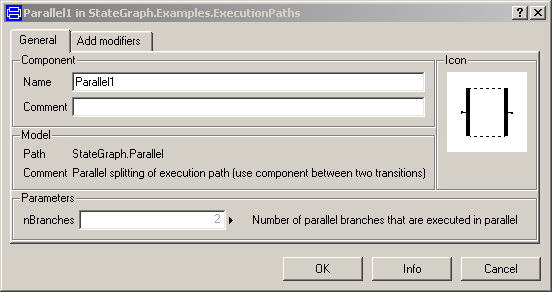
Parallel, Alternative and Step components have vectors of connectors. The dimensions of these vectors are set in the corresponding parameter menu. E.g. in a "Parallel" component:

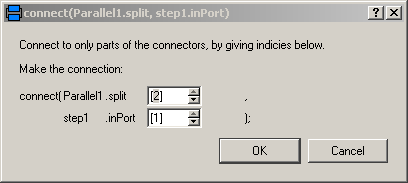
Currently in Dymola the following menu pops up, when a branch is connected to a vector of components in order to define the vector index to which the component shall be connected:

CompositeSteps, Suspend and Resume Port

A StateGraph can be hierarchically structured by using a CompositeStep. This is a component that inherits from PartialCompositeStep. An example is given in the next figure (from Examples.ControlledTanks):

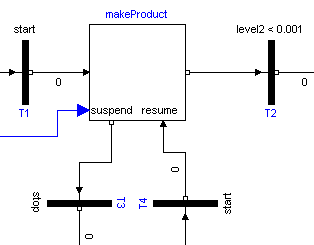
The CompositeStep component contains a local StateGraph that is entered by one or more input transitions and that is left by one or more output transitions. Also, other needed signals may enter a CompositeStep. The CompositeStep has similar properties as a "usual" step: The CompositeStep is active once at least one step within the CompositeStep is active. Variable active defines the state of the CompositeStep.

Additionally, a CompositeStep has a suspend port. Whenever the transition connected to this port fires, the CompositeStep is left at once. When leaving the CompositeStep via the suspend port, the internal state of the CompositeStep is saved, i.e., the active flags of all steps within the CompositeStep. The CompositeStep might be entered via its resume port. In this case the internal state from the suspend transition is reconstructed and the CompositeStep continues the execution that it had before the suspend transition fired (this corresponds to the history ports of StateCharts or JGrafcharts).

A CompositeStep may contain other CompositeSteps. At every level, a CompositeStep and all of its content can be left via its suspend ports (actually, there is a vector of suspend connectors, i.e., a CompositeStep might be aborted due to different transitions).