Rotation
2D/3D• Rotation[bnum] returns the angle of rotation (2D) or the angle and axis of rotation (3D) of body bnum.
• Rotation[{ei, ej}] (2D) or Rotation[{eo, ei, ej, ek}] (3D) returns the angle-axis of rotation associated with the given Euler parameters.
• Rotation[matrix] returns the angle or angle-axis of rotation associated with the given 2D or 3D rotation matrix. • In Modeler2D, Rotation returns scalar angle of rotation 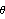 . .
• In Modeler3D, Rotation returns the angle-axis of rotation in the form: {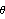 , {x, y, z}}. , {x, y, z}}.
• In Modeler2D, if the Euler solution method is specified with SetSymbols, Rotation[bnum] returns the angle of rotation in terms of Euler parameters. With the Angular solution method Rotation[bnum] simply returns  bnum. bnum.
• In Modeler3D, Rotation[{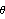 , vector}] returns the given angle-axis after potentially normalizing the axis and transforming it to the global reference frame. , vector}] returns the given angle-axis after potentially normalizing the axis and transforming it to the global reference frame.
• In Modeler3D, Rotation[vector] returns the angle-axis of rotation associated with the given virtual rotation vector.
• When Rotation is used to transform a virtual rotation or an angle-axis, vector may be a simple vector or a Mech vector object with head Vector, Line, or Plane.
• In Modeler3D, the Normalized option can be given to determine whether the resulting axis of rotation is normalized. The default setting is Normalized->True.
• With Normalized->True an Indeterminate result is returned for the axis of rotation if the angle of rotation is zero.
• See also: Alpha, Angle, EulerParameters, Omega, Origin, RotationMatrix, VirtualRotation. Further Examples Load the Modeler2D package. Here is the rotation angle of body 2.
Out[2]= | 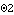 |
If we switch to Euler coordinates then the rotation angle is expressed in terms of Euler parameters.
Out[4]= | 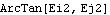 |
Rotation can be used to change other representations of rotation--Euler parameters or a rotation matrix--into a rotation angle.
Out[5]= | 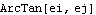 |
Out[6]= | 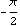 |
Load the Modeler3D package. Here are the angle and axis or rotation of body 2 expressed in terms of Euler parameters.
Out[8]= | 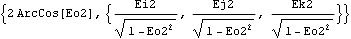 |
Rotation can be used to change Euler parameters, a rotation matrix, or a virtual rotation vector into a rotation angle.
Out[9]= | 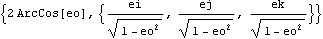 |
Out[10]= | 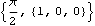 |
Out[11]= | 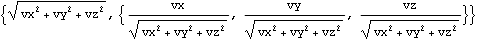 |
|